vol. 58 num. 4 octubre - diciembre 2007
Portada
|
||||||||||
EditorialJuan Pedro Laclette
|
||||||||||
Índice 58-4
|
ciencia |
|
|
octubre-diciembre 2007 volumen 58 número 4 |
|
|
comunicaciones libres |
|
Reflexiones sobre la investigación en arquitectura Fernando N. Winfield Reyes La precisión en los cálculos científicos por computadora Edscott Wilson García y Guillermo Morales-Luna Pinzas ópticas: las delicadas manos de la luz Karen Volke Sepúlveda, Ibis Ricárdez Vargas y Rubén Ramos García La codificación de los quipus incas Hugo Cabrera Ibarra, Haret Rosu Barbus, Luís Adolfo Torres González y Juan Pablo Treviño Gutiérrez El desierto y sus habitantes: el caso de la hormiga roja Rafael Guzmán Mendoza Las selvas tropicales y el cambio climático Julián Granados Cambio de uso del suelo y degradación ambiental Leopoldo Galicia Sarmiento, Arturo García Romero, Leticia Gómez-Mendoza y M. Isabel Ramírez Selva seca y sequía: compañeras inseparables Mirna Valdez-Hernández, Elizabeth Ma. Osorio-Gil, Paula Jackson y José Luís Andrade |
editorial Juan Pedro Laclette
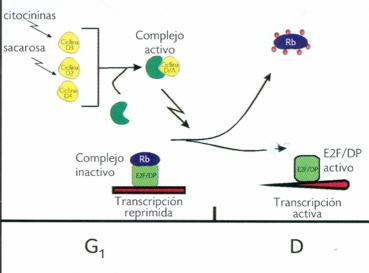
Beneficios de los sistemas agroforestales: amor por nuestras tierras El control del ciclo celular en plantas ¿Para qué sirve la endogamia? Los tribunales constitucionales y la división de poderes debate |
Editorial
Editorial
Para la Academia Mexicana de Ciencias (amc), la educación, la investigación, el desarrollo y la innovación forman una cadena de valor para impulsar el desarrollo del país en un mundo dominado por el conocimiento.
Por ello, la AMC dedica un esfuerzo considerable a sus programas de educación, promoción y divulgación de la ciencia, como Domingos en la ciencia, Computación para niños, Veranos en la ciencia, Olimpiadas de l a ciencia, La ciencia en tu escuela, y Pauta, que juntos tienen un impacto considerable a lo largo y ancho del país.
En esta ocasión destacaré el programa de Olimpiadas, que promueve el interés de los jóvenes a través de competencias del conocimiento. Actualmente, la AMC coordina las Olimpiadas de Biología y Química, que se organizan desde 1999; la Olimpiada de Geografía, que se organiza desde 2002, y la Olimpiada de Historia de México, que se organizó por primera vez en 2007. Además, la AMC organiza el Concurso de primavera y la Competencia cotorra de matemáticas. En conjunto, estas competencias convocan cada año a cientos de miles de niños y jóvenes en todo el país.
Los ganadores de los concursos nacionales forman las delegaciones que representan a México en competencias internacionales. Hace apenas unas semanas se celebraron las Olimpiadas Internacionales de Biología y Química, así como el Campeonato Mundial de Geografía de National Geographic y la Olimpiada Regional Asia-Pacífico de Geografía. Los resultados de las delegaciones mexicanas fueron excelentes. En el Campeonato Mundial de Geografía, México obtuvo el primer lugar absoluto. En la Olimpiada Regional Asia-Pacífico de Geografía, el equipo mexicano también ganó el primer lugar. En la Olimpiada Internacional de Biología se obtuvieron dos medallas de bronce y en la de Química una mención honorífica.
Por supuesto, debemos resaltar el talento de nuestros jóvenes premiados: nos sentimos muy orgullosos de sus triunfos, que nos permiten vislumbrar una generación altamente competitiva. Estos triunfos, que han sido muy publicitados en fechas recientes, son sólo la "punta del iceberg"; detrás de ellos está el trabajo de muchos profesores, de los coordinadores y organizadores de estas competencias, y los generosos patrocinios de instituciones públicas y privadas que permiten su realización. Para dar una idea de la magnitud del trabajo, mencionaré que todas nuestras competencias se llevan a cabo en diferentes etapas (locales, estatales y nacionales). En la etapa local, contamos con el apoyo de cientos de maestros que inscriben a los niños y jóvenes y que aplican los exámenes, ciudad por ciudad, estado por estado. En la segunda etapa se lleva a cabo el concurso a nivel estatal, contando para ello con una valiosa red de delegados en los estados de la República. Finalmente se lleva a cabo la etapa nacional, generalmente apoyada por universidades públicas de los estados.
Las Olimpiadas de la Ciencia son un ejemplo de lo que se puede lograr sumando esfuerzos y talentos de muchas personas e instituciones e invirtiendo en el futuro de México, que son sus niños y jóvenes.
Juan Pedro Laclette
Presidente de la AMC
Reflexiones sobre la investigación en arquitectura
Reflexiones sobre la investigación en arquitectura
Fernando N. Winfield Reyes
![]()
Actitudes y procesos de conocimiento
La investigación es un proceso sistemático y ordenado que busca entender la realidad para poder interactuar con ella y a la larga transformarla, ahí donde se detectan problemas por resolver. De manera genérica se concibe a la investigación como una indagación, el seguimiento de un determinado interés, o bien la definición, propuesta y determinación de una solución a un problema específico con límites más o menos precisos. La investigación debe ser consciente, sistemática, ordenada, útil. Debe plantear retos y metas posibles, de tal suerte que no se vuelva motivo constante de frustración. La importancia de la investigación en las sociedades modernas es evidente, pues mediante el desarrollo de la ciencia, la tecnología, las humanidades y las artes ha sido posible alcanzar mayores niveles de bienestar y desarrollo.
Para ser investigador no se requiere en realidad un entrenamiento especial, grados académicos o títulos de especialización, sino más bien una actitud de curiosidad, objetividad, interés por la verdad y tenacidad, que es la disposición a sufrir muchos reveses y a pesar de ello seguir adelante con motivación y convicción en el proceso de una idea.
En suma, la investigación es curiosidad con sistema, con un seguimiento ordenado la mayor parte de las veces, basado en la intuición y en las intenciones y -para gran parte de las iniciativas en arquitectura-, en la razón del proyecto. Se trata de investigar no sólo para publicar, sino para difundir y extender el conocimiento, aportando nuevas soluciones creativas.
Pasado y presente en la investigación en arquitectura
La investigación en arquitectura todavía no tiene un estatus muy preciso, y constituye un ámbito de discusión y polémica. Si uno recurre por ejemplo a la clasificación que establece en México el Consejo Nacional de Ciencia y Tecnología (Conacyt), se la coloca entre las ciencias del comportamiento, aunque atendiendo a otros criterios, en ocasiones se nos ubica en los campos de la ingeniería, las disciplinas ambientales, el desarrollo urbano, las humanidades o incluso las artes. Esto genera en ocasiones ambigüedad y dificultad para que se reconozca con claridad la investigación en arquitectura, sus resultados y sus productos, sobre todo cuando se la somete a criterios derivados del análisis de otras disciplinas, o cuando criterios distintos se tratan de encajar en nuestro quehacer sin que esto sirva mucho para darle un sentido preciso a las características especiales de la investigación arquitectónica.
No obstante, ya desde el texto más antiguo que por ahora conocemos sobre teoría de la arquitectura, denominado Los diez libros de arquitectura, escrito por Vitrubio, arquitecto romano del siglo I de nuestra era, se establecen una serie de actitudes y aptitudes necesarias para esta profesión, entre las que podemos ubicar la idea de investigar. Los diez libros, desde una perspectiva histórica, constituyó la base para teorías más elaboradas aplicadas a la edificación, y su registro de los órdenes clásicos posibilitó el conocimiento e interpretación de las proporciones clásicas, aunque por su carencia de ilustraciones originales se ha prestado a una multitud de interpretaciones y confusiones. Vitrubio reconoce que la arquitectura, al igual que otras artes, se compone de una parte teórica y otra práctica, y que es necesario que quien la ejerza conozca de ambas; advierte además que el arquitecto no se debe limitar sólo a los conocimientos relativos a la arquitectura, sino que debe poseer conocimientos de otras disciplinas a propósito de poder operar en el mundo complejo en el que se desarrolla su actividad. Su tratado atiende entonces a una variedad de conocimientos que no sólo se limitan a nociones de teoría de la arquitectura y de edificación, sino que incluyen elaboradas descripciones en torno a la ubicación de asentamientos de población, obras de ingeniería hidráulica, construcción de murallas y fortificaciones, embarcaciones, artefactos de guerra e incluso astrología.
Como advocaciones para el sentido de la investigación en la arquitectura, la trilogía vitrubiana del utilitas (utilidad), vetustas (gracia, decoro y belleza) y firmitas (solidez constructiva) constituye un buen punto de partida.
A lo largo de la historia de la arquitectura, la idea de investigar ha cambiado. La manera de concebir la arquitectura y los atributos de su esencia, el espacio y la forma, se han ido transformando a partir de un conjunto de conceptos que en las escuelas de arquitectura y en los centros de enseñanza de posgrado se han asociado a la historia y a la teoría y práctica de la arquitectura.
Hace unas semanas, en uno de esos días en los que la madrugada nos desvela, revolviendo libros y revistas recientemente adquiridas, llegué un tanto al azar a un artículo que acabó por ser una ventana formidable a la manera emocionante e intensa en la que un arquitecto francés contemporáneo, Paul Andreu, famoso por sus extraordinarias soluciones a las terminales de transporte del aeropuerto Charles de Gaulle de París y el de Shanghai-Pudong, donde la simplicidad esencial es eco de contemporaneidad, comparte sus reflexiones sobre su experiencia sobre el proyecto y la arquitectura, estos términos que en ocasiones acaban por ser sinónimos de existencia. Mientras leía a Andreu surgió esta pregunta: ¿Cómo responder desde la arquitectura, vocación y elección de vida, a un mundo cambiante, por demás complejo y cada vez más elusivo?
|
|
| Torso en giro, el edificio residencial más alto de Suecia y uno de los más altos de Europa, obra del arquitecto Santiago Calatrava. |
Dice nuestro autor de referencia que en su voluntad por integrar las diversidades a un pensamiento conjunto, cada vez más general y a la vez más complejo, fue hallando su propia coherencia de ideas y claridad en la determinación de sus proyectos. Comenta que precisamente al mirar de un modo distinto los objetos y su relación con el entorno, al dejar madurar las soluciones espaciales para distintas funciones cambiantes, fue llegando al entendimiento del tiempo como uno de los materiales de la arquitectura. Acaso es en este afán de conciencia en el que podremos ir construyendo la madurez, el equilibrio, el desarrollo, la mejora constante de nuestros modos de producir soluciones desde el proyecto.
Otro tema importante es la capacidad de adaptación, la flexibilidad; una nueva arquitectura que habrá de surgir del detalle lo mismo que de la generalidad o el esquema de conjunto, encontrando que la arquitectura, como ejercicio existencial, consiste en un desarrollo continúo: una capacitación constante para enriquecerse con una evolución de ideas y formas. Finalmente, aconseja Andreu nunca buscar la originalidad a ultranza, sino más bien "explorar e investigar los terrenos que ignoramos".
Y aquí conecto con la intención de estas reflexiones: la investigación, como actitud existencial, como disposición profesional, no es la solución a todos los problemas, pero nos marca caminos a seguir, modos de exploración, interrogantes. En ocasiones, más que respuestas inmediatas, lo que genera son las posibilidades de nuevas ideas y nuevos conceptos: es nuestra voluntad de interrogarnos y buscar soluciones. Así, la investigación es como un motor que se tiene que mantener actualizado y a la vanguardia profesional, independientemente del campo de estudio específico en el que uno decida incursionar.
 ¿Que investigar? ¿Cómo investigar? La motivación y el interés como actitudes centrales
¿Que investigar? ¿Cómo investigar? La motivación y el interés como actitudes centrales
Cualquier tema de investigación puede ser interesante. Lo importante es un conjunto de actitudes personales. Se requieren, además, elementos de originalidad, innovación y viabilidad operativa o constructiva.
Un elemento fundamental es romper con los mitos de la investigación para el caso de la arquitectura, la manera en que ésta se concibe como recipiente de actividades propias sólo de los laboratorios o los centros de alta especialización tecnológica, e interesar a la gente: al mayor número posible. La investigación en arquitectura puede nutrir nuestro conocimiento del mundo, abriendo nuevos horizontes a los paradigmas tradicionales.
Se trata de buscar compartir experiencias, conocer cosas nuevas, prácticas eficientes; por ejemplo, qué se ha hecho en otros ámbitos, contextos o culturas, buscando decidir qué se puede replicar, adaptar a un medio o condiciones locales, y qué no... y en todo ello se observa siempre que la motivación a investigar es el ingrediente central.
Ámbitos de la investigación en arquitectura y disciplinas afines
La investigación debe tener la visión de futuro. Es importante proyectar no sólo tratando de adivinar al azar caminos posibles o convencionales, sino que es fundamental dar certidumbre. Un ejemplo de ello son las nuevas alternativas de generación de energía que están transformando la arquitectura, el espacio, la naturaleza de sus funciones y el contenido de su enseñanza en programas tradicionales. Aspectos como el uso lógico del sol, la lluvia, el suelo y el viento serán cada vez más un tema central en el diseño de nuevas formas y soluciones en un contexto donde la energía es cada vez más un bien cuyas fuentes parecen limitadas.
|
|
| Le Corbusier con la maqueta del Plan Voisin, París (1925). Imagen reproducida de la película L'architecture d'aujourd'hui, de Pierre Chena (1931). La utilización de dibujos, esquemas y modelos tridimensionales o maquetas ha sido a lo largo de la historia uno de los procesos para generar desde la teoría y la práctica de la arquitectura propuestas visionarias y modelos de utopías, lo mismo que elementos que pueden ser comprobados experimentalmente antes de su construcción (Smith, 2004). |
La investigación habrá de situar riesgos y amenazas. La arquitectura está inmersa en todos los escenarios, independientemente de nuestros postulados de forma y función. Hoy es importante comenzar a enfocar nuestros proyectos con nuevas ideas acerca de la tecnología, por ejemplo, o los desarrollos más recientes de integración con otras disciplinas como la domótica (conjunto de sistemas capaces de automatizar una vivienda, aportando servicios de gestión energética, seguridad, bienestar y comunicación), las energías alternativas, los materiales con nuevas y sorprendentes propiedades, las formas que respondan con mayor flexibilidad a necesidades crecientemente complejas en donde la búsqueda de un balance entre entornos naturales y artificiales se pueda crear desde el enfoque de la sustentabilidad como un modelo viable de una filosofía del existir.
Otras áreas de investigación de frontera se refieren también a la geografía, la ciencia política, la psicología y la sociología, para dar respuestas más adecuadas a las necesidades diversas de individuos, grupos y colectivos, integrando el saber de la arquitectura y estableciendo puentes conceptuales y prácticos con las disciplinas sociales y humanísticas. No hay que olvidar que la esencia de la arquitectura, el ser humano, obliga a considerar que entre los deberes profesionales del arquitecto está la consecución de espacios que reflejen las aspiraciones, la cultura y el pensamiento, y generen un confort en las percepciones de los espacios del hábitat. Nuevas aproximaciones a problemas como la falta de una vivienda adecuada y digna para millones de familias y el desarrollo de asentamientos progresivos que mejoren las condiciones de vida precaria de un porcentaje significativo de la población de regiones, países y continentes es una de las agendas centrales para el desenvolvimiento de la arquitectura y disciplinas afines en los próximos años, como se desprende de una revisión de la diversidad de propuestas generadas y discutidas en torno al XXII Congreso Mundial de Arquitectos, celebrado en Estambul en 2005 (Unión Internacional de Arquitectos, 2005).
|
La Ciudad de las Artes y las Ciencias, en Valencia (España), ciudad que hace honor a su nombre por sus contenidos. Se trata de un espacio público en el que los arquitectos Santiago Calatrava y Félix Candela despliegan sus saberes técnicos y artísticos. |
La importancia de los programas de posgrado se relaciona con la capacidad de motivar preguntas e interrogantes interesantes, y encontrar en este ámbito la oportunidad de conocer bajo un propio postulado soluciones apropiadas. Por ello la investigación y el posgrado son entornos mutuamente benéficos.
De ahí que la innovación sea el medio a través del cual se puede trascender en lo económico, lo social y lo ambiental. Circunstancias que desenvuelven un concepto, llámese arquitectura o urbanismo, construcción, diseño o tecnologías para el habitar.
Dondequiera que vayamos, siempre estaremos en contacto con la arquitectura. Incluso con arquitecturas vivas. La investigación habrá de situarse siempre en el contexto, buscando un balance entre las tecnologías de punta y los aspectos regionales de operación básica.
Como filosofía de la investigación en la arquitectura, puede decirse que el espacio es un medio formidable de educación. Desde esta premisa, un espacio puede contribuir a complementar la formación y a elevar el nivel de vida. Investigar la condición del espacio y su situación contemporánea es motivo central del proyecto en arquitectura. Proyecto y destino.
El futuro de la investigación en la arquitectura estará siempre en la creatividad, en lo posible desde la lógica constructiva, en la invención y la utopía como motivación permanente; en la investigación aplicada al desarrollo y a la tecnología como inspiración del espacio.
Indudablemente, hay ámbitos de investigación en la arquitectura, como la teoría y la historia, los aspectos tecnológicos, los sistemas y nuevos materiales, las formas inéditas y las modalidades nuevas de agrupación, ideación y expresión gráfica; la interrelación con otras ciencias y campos disciplinares, por mencionar algunos entornos. En ellos se irá ganando credibilidad social y autonomía técnica en los próximos años, generando mayor confianza y un estatus más definido y reconocido para nuestra profesión y para las soluciones que desde el proyecto se aporten como base para nuevas y estimulantes líneas de investigación y generación de conocimientos. En este sentido, resulta estimulante observar que la Unión Internacional de Arquitectos (UIA), organismo que integra alrededor de 1 millón 300 mil arquitectos en todo el mundo, plantea en la actualidad el reconocimiento al proyecto y a las experiencias sistemáticas que se derivan de éste como un campo de investigación cuya pertinencia social será cada vez mayor.
 Como señala Okasha (2002, p. 134) en torno al papel de la ciencia en la sociedad contemporánea, la crítica y la reflexión son necesarias para garantizar que los impactos del desarrollo tecnológico, humanístico y artístico (como prácticamente todas las disciplinas que tienen injerencia en la vida cotidiana, y entre ellas la arquitectura) se dirijan hacia condiciones de mejora e innovación.
Como señala Okasha (2002, p. 134) en torno al papel de la ciencia en la sociedad contemporánea, la crítica y la reflexión son necesarias para garantizar que los impactos del desarrollo tecnológico, humanístico y artístico (como prácticamente todas las disciplinas que tienen injerencia en la vida cotidiana, y entre ellas la arquitectura) se dirijan hacia condiciones de mejora e innovación.
En suma, la condición de pluralidad del mundo contemporáneo tiene implicaciones para la arquitectura, si se entiende a ésta como la profesión que conforma el medio construido y, en consecuencia, no está exenta de un importante papel en la transformación de la sociedad; contenido ético que conlleva una enorme responsabilidad.
Bibliografía
Frampton, K. (1992), Modern architecture. A critical history, Londres, Thames and Hudson.
Vitrubio, M. (1999), Los diez libros de arquitectura, Madrid, Alianza.
Okasha, S. (2002), Philosophy of Science. A very short intr-duction, Oxford, Oxford University Press.
Roy, M. y P. Andreu (2002), Paisajes de la movilidad, presen¬tación de S. Topelson, introducción y traducción de L. Noelle, colección Cuadernos de Arquitectura, vol. 7, México, Dirección de Arquitectura y Conservación del Patrimonio Artístico Inmueble, Consejo Nacional para la Cultura y las Artes e Instituto Nacional de Bellas Artes.
Smith, A. C. (2004), Architectural Model As Machine, A New View Of Models From Antiquity To The Present Day, Oxford, Architectural Press.
Union International de Arquitectos (2005), XXII World Congress of Architecture UIA 2005, Istanbul. Cities: Grand bazaar of architectures. Abstracts, Estambul, UIA/Colegio de Arquitectos de Turquía/Municipalidad Metropoli-tana de Estambul.
Fernando N. Winfield Reyes es miembro del Sistema Nacional de Investigadores. Sus trabajos de investigación a nivel maestría y doctorado han sido distinguidos en la Tercera y Sexta Bienales de Arquitectura Mexicana (1994 y 2000). Ha participado en diversos proyectos de investigación teórica y aplicada. Cuenta con más de treinta publicaciones en el ámbito de la arquitectura y el urbanismo. Esta dirección de correo electrónico está siendo protegida contra los robots de spam. Necesita tener JavaScript habilitado para poder verlo.
La precisión en los cálculos científicos por computadora
La precisión en los cálculos científicos por computadora
Edscott Wilson García y Guillermo Morales-Luna
![]()
Introducción
¿Cuánta gente confía ciegamente en los resultados que arroja una computadora? ¿Qué peligro plantean para la precisión de los cálculos científicos realizados por computadora las velocidades de procesamiento cada vez mayores? En casi todas las ramas de la ciencia, si no es que en todas, se utiliza alguna expresión numérica que involucra cálculos. Aún la más rebuscada ecuación científica, si dispone de solución numérica, se resuelve con operaciones aritméticas fundamentales. Pero como todas las herramientas construidas por el ser humano, la computadora tiene sus limitaciones.
Durante la Guerra del Golfo, el 25 de febrero de 1991, un projectil Scud iraquí hizo blanco en la base militar de Dahrahn en la Arabia Saudita, matando a veintiocho soldados: falló el intento de intercepción del cohete Patriot. Posteriormente se condujo un estudio para determinar las causas de la falla: el sistema de control tenía un contador en incrementos de una décima de segundo. Mediante punto flotante, en la base binaria utilizada por la computadora, 0.1 tiene un patrón fraccionario que se trunca. Consecuentemente, la precisión de 24 bits del sistema Patriot, tenía un error de diez millonésimas de segundo en su contador de tiempo. Al cabo de cuatro días el error se acumuló hasta llegar a un tercio de segundo, lo cual implicó una desviación de 700 metros. Para efecto de intercepción del projectil Scud, un error de 700 kilómetros hubiera producido el mismo resultado final.
En el Centro de Estudios Avanzados del Instituto Politécnico Nacional (Cinvestav) y el Instituto Mexicano del Petróleo (imp), así como en el Lawrence Berkeley National Laboratory en Estados Unidos, y el Institut National de Recherche en Informatique et en Automatique, en Francia, entre otros centros de investigación, se ha trabajado en el problema de la realización de cálculos digitales científicos con precisión certera, es decir, la obtención de resultados en los cuales se puede afirmar con certidumbre hasta qué dígito decimal el resultado es verdadero. Para el laboratorio de cómputo, la precisión certera es análoga a lo que se conoce en química como "cifras significativas", un dato indispensable para todos los análisis de laboratorio.
Aunque existen paquetes numéricos como Matemática (Wolfram) y Maple (Maplesoft) con los que se pueden resolver algoritmos con precisión arbitraria o números racionales exactos, su funcionamiento de "caja negra" no permite verificar que las operaciones se hagan de manera correcta, óptima o adecuada al problema en particular. Para el investigador es fundamental tener la capacidad de verificación de los resultados. Por ende, el cómputo científico hoy en día se hace en su mayor parte con los lenguajes FORTRAN y C. El propósito de este artículo es describir cómo puede trabajar un programador científico para lograr mejor precisión utilizando cualquiera de estos lenguajes.
¿Cuál es la precisión?
La precisión computacional está determinada primariamente por la cantidad de dígitos con los que se efectúan las operaciones aritméticas, conocida a partir de la longitud de palabra del procesador. La palabra establece el número entero más grande que se puede representar con exactitud. En el procesador Intel modelo 8088, por ejemplo, se tenía una longitud de ocho bits, que proporcionan un entero máximo de 256. Concatenando dos palabras de este procesador (precisión doble) se pueden obtener cuatro cifras decimales significativas. Como se puede observar en el Cuadro 1, el tamaño de la palabra, y por ende la precisión, ha ido en constante aumento.
Cuadro 1. Dígitos de precisión decimal para operaciones con números enteros con respecto de la velocidad y tamaño de palabra.
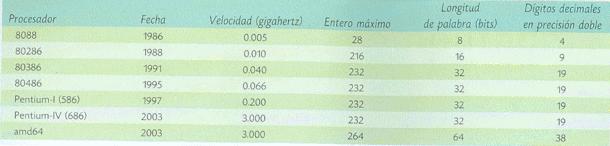
Para un procesador con una longitud de palabra de 32 bits se obtienen 19 dígitos decimales en precisión doble, mientras que para los procesadores de 64 bits -de última generación- se obtienen 38. Generalmente una decena de dígitos decimales es suficiente para la mayoría de los propósitos de cálculo. El advenimiento de la tecnología láser implica que se pueden realizar mediciones sobre objetos del mundo físico con un creciente grado de exactitud. Esta información requiere de mayor precisión en los cálculos computacionales.
Al efectuar cada operación aritmética se reduce, por cuestiones de redondeo y truncamiento, el número de dígitos significativos del resultado final. Cualquier operación aritmética sobre un número x para obtener un resultado y incurre obligatoriamente en un error de redondeo, Exy. Consecuentemente, si el valor x representa una cantidad con una tolerancia ±d, en el resultado será de ±E con E = d+ Exy. Muchos algoritmos de cálculo, como los métodos de Newton-Raphson y Runge-Kutta para resolver numéricamente ecuaciones diferenciales que aparecen en los modelos de simulación de plantas y procesos de refinación, son sujetos a una serie repetitiva de operaciones donde los resultados se vuelven a alimentar como datos en cada iteración. ¿Hasta qué punto afectarán estos errores de redondeo el resultado final? Eso no es sencillo de contestar, ya que el cálculo del error supera en complejidad al problema numérico. ¿Qué se puede hacer al respecto?
Por un lado se puede adquirir un procesador con tamaño de palabra superior para trabajar con representaciones numéricas de mayor longitud, pero un vistazo al Cuadro 1 es suficiente para constatar que esto es insuficiente. Nótese que la velocidad del reloj de los procesadores ha ido en constante aumento, pero la razón de crecimiento en tamaño de palabra no ha sido equiparable. En menos de veinte años, el hardware de los procesadores multiplicó la velocidad de procesamiento por 600, mientras que la precisión de las operaciones -determinada por el tamaño de palabra-aumentó tan sólo cuatro veces. La parte faltante del aumento de precisión en el hardware debe ser suplida por métodos de software cada vez más complejos. Al aumentar la velocidad de procesamiento también se abrió la posibilidad de aplicar métodos numéricos más sofisticados, con un creciente número de operaciones aritméticas. Ello también aumenta los errores por redondeo.
Un ejemplo donde la precisión juega un factor importante es la exploración petrolera. Para la prospección geofísica se utiliza un modelo matemático basado en inducir ondas sísmicas y analizar los resultados mediante la ecuación de onda. Con esto es posible predecir la forma de las capas de roca bajo la superficie. Pero los datos que se alimentan son cuantiosos, y el número de operaciones que se tienen que realizar, muy elevado. Suelen pasar días antes de obtener un resultado utilizable. La falta de precisión en mediciones y pérdida de precisión en operaciones aritméticas induce un margen de error, que cuando se aplica a la selección de sitios para la perforación de pozos puede llegar a costar millones de dólares. El aumento en la velocidad de los procesadores ha hecho que el tiempo para obtener los resultados vaya disminuyendo constantemente, pero los resultados no son más exactos.
El error relativo se refiere al error de redondeo que se presenta en cada resultado parcial al efectuar una operación aritmética, y afecta todas las operaciones subsecuentes que utilizan el resultado parcial como operando. Los errores relativos se acumulan, y cada resultado parcial tiene asociado un error relativo total. Algunos métodos para estimar los errores inducidos se encuentran descritos en el trabajo de Miller y Spooner (1975), donde se verifica que el análisis de error eleva al cuadrado la complejidad del algoritmo numérico. Por dicho motivo, en la práctica el análisis de error nunca se lleva a cabo.
Entonces, ¿qué se puede hacer en cualquier rama científica donde hay necesidad de exactitud en los cálculos para garantizar que los resultados tengan la precisión requerida y no son simplemente iteraciones sobre errores de redondeo?
Las metodologías para acotar el error incluyen la precisión arbitraria (donde se extiende hasta el límite de la máquina la memoria utilizada para almacenar los dígitos), los números racionales (donde en lugar de utilizar un punto flotante se almacenan dos números enteros para representar el cociente, p/q), la aritmética de intervalos (donde se va modificando un intervalo de confianza), y la aritmética de rangos (donde el intervalo de confianza determina de manera dinámica a la precisión arbitraria).
El lenguaje
Cuando el investigador busca precisión en los cálculos, deberá cambiar la aritmética con la que se efectúan las operaciones escogiendo el método que más convenga. La utilización de cualquier método para incrementar la precisión implica un aumento en la cantidad de operaciones que se efectúan en el procesador. Por tanto, es imperativo escoger el lenguaje de programación idóneo. Una de las desventajas del FORTRAN es que permite la programación no estructurada, la cual tiende a producir código ejecutable menos eficiente. Por ello, el programador que utilice este lenguaje deberá poner especial cuidado en utilizar la sintaxis estructurada. Para el programador en C este detalle no es tan importante, ya que el lenguaje mismo es estructurado. Sin embargo es importante que se considere el uso de FORTRAN cuando se cumplen las dos siguientes condiciones:
El investigador dispone de un compilador de FORTRAN-95 optimizado para la arquitectura del hardware (por ejemplo, Lahey/Fujitsu para Windows/ Linux/ Solaris).
El algoritmo de cálculo involucra aritmética vectorial/matricial y los resultados de la aritmética matricial en precisión doble no acarrea un error que pudiese ser significativo (es decir, algoritmos con ciclos de iteración breves).

Cuando se cumplen estas dos condiciones, entonces es aconsejable la utilización de FORTRAN-95 para aprovechar las funciones MATMUL, TRANSPOSE, PRODUCT, SUM, MAXVAL y otras que generan código binario optimizado. Cuando se trabaja únicamente con aritmética escalar, es posible generar binarios más eficientes con C, y la selección del lenguaje se convierte en una preferencia del programador. Los programadores científicos de instituciones como el National Center for Supercomputing Applications (NCSA), el Los Alamos National Laboratory (LANL), y el Argonne National Laboratory (anl), por citar unos cuantos ejemplos estadounidenses, han obtenido buenos resultados combinando los dos lenguajes, ya que las instrucciones de FORTRAN-95 y C++ se pueden enlazar en el programa ejecutable final. Una vez definido el lenguaje, resta determinar la metodología. Es aconsejable para el programador científico no partir de cero, sino aprovechar el código ya escrito y comprobado que puede incorporar directamente en sus programas, o conjuntar en el paso de enlazamiento del código máquina.
Lo arbitrario
La precisión arbitraria es una extensión del formato IEEE de punto flotante que permite almacenar una cantidad variable de dígitos. Esta modalidad se limita únicamente por la capacidad de memoria de la computadora. Los números de precisión arbitraria se expresan mediante un vector de palabras, donde cada elemento representa una porción de dígitos de la mantisa, expresado en términos de una base numérica. La base utilizada es la que más convenga de acuerdo a la arquitectura del procesador; comúnmente, el máximo entero mostrado en el Cuadro 1. Por ejemplo, en una computadora de 32 bits la base sería B=232. Algunas computadoras son capaces de efectuar operaciones aritméticas de punto flotante con más velocidad, y hay quien prefiere utilizar una base expresada en términos de un número de tipo punto flotante.
En la aritmética se aplican los métodos clásicos. Pero cuando los números de precisión múltiple rebasan varios miles de dígitos, se puede lograr una aceleración en la multiplicación aplicando el método de Karatsuba, o bien haciendo una conversión a aritmética modular y aplicando transformadas rápidas de Fourier. Estas dos técnicas están descritas en el texto clásico de Knuth (1981).
Al efectuar una multiplicación de dos números de n dígitos, el producto que se obtiene consta de 2n dígitos, de los cuales se desecharán n. Es posible acelerar el proceso de multiplicación si los dígitos sobrantes no se incluyen dentro del algoritmo de multiplicación desde un principio. Sin embargo, no es conveniente desecharlos todos, ya que esto implicaría un mayor error en el redondeo final. Los dígitos a partir del n+1, conservados para el proceso de multiplicación -y que se desecharán después del redondeo final-, se llaman dígitos de guardia.
Existe una larga trayectoria en el desarrollo de código de este tipo del cual puede hacer uso el investigador en sus programas. Comienza con el trabajo MP (Multiple Precision) de Brent (1978). MP fue el primero que era independiente de la arquitectura del procesador y que contaba con rutinas para funciones especiales (ln, exp, sin) y constantes irracionales. Funciona con un vector de enteros de precisión sencilla. Entre las funciones de MP encontramos la conversión de valores enteros, reales y doble precisión a formatos MP y viceversa; operaciones aritméticas fundamentales, la elevación de potencias y cálculo de raíces. El código está escrito en FORTRAN, y en la Universidad de California, Bailey (1995) hizo la conversión a FORTRAN-90 con lo cual se permite implementar el código de una manera más natural. Y en el 2002 construye la interfase C++ para mejorar los algoritmos y desempeños, rebautizándolo con el nombre de ARPREC. Para el programador científico, el código fuente de ARPREC es de acceso libre en el sitio http://crd.lbl.gov/~dhbai-ley/mpdist/ para su inclusión en programas de cómputo de investigación en FORTRAN-95 o C++.
ARPREC representa un esfuerzo norteamericano por facilitar los cálculos digitales con precisión. Por otro lado tenemos GMP, que representa un esfuerzo europeo. Este código está disponible en http://www.swox.com/gmp/ .La meta de GMP es la de proporcionar el código con mayor velocidad de ejecución y mejor desempeño. Para ello se vale de código especial para los distintos tipos de procesadores. Su utilización en programas de cómputo de investigación es libre, así como su utilización en proyectos comerciales.
GMP es sustancialmente más rápido que ARPREC, tiene implementada la aritmética racional y existe código compatible para realizar aritmética de intervalos. Su interfase es de C y FORTRAN-77. ARPREC, por otro lado, es compatible a C++ y FORTRAN-95 y dispone de todas las funciones vectoriales y matriciales intrínsecas que lo hace una poderosa herramienta. No es difícil construir un ejecutable que haga uso de ambas bibliotecas de manera simultánea, si el algoritmo así lo requiere.
Lo racional
Los números racionales son aquellos que se pueden expresar como el cociente de dos números enteros, p/q. Para la codificación de estos números, se almacenan dos variables enteras de precisión arbitraria por cada número. Después de cada operación aritmética, se reducen estos enteros con su mayor común divisor para evitar que crezcan de manera innecesaria. Los enteros p y q se manejan de manera exacta. En el momento en que la memoria de la computadora sea insuficiente para expresar a p o q con todos sus dígitos, el cálculo se detiene con un mensaje de error. Por tanto, si el programador científico desea exactitud, la aritmética racional es una buena opción. Pero si sólo desea tener certeza de la precisión, puede optar por una metodología de aritmética de intervalos.
Los intervalos
Con la aritmética de intervalos cada número real se aproxima por dos números con representación digital exacta, y la aritmética se efectúa sobre estas parejas. El primero representa una cota inferior y el segundo una cota superior.
La aritmética de intervalos es importante por las siguientes razones:
• Puede ser utilizada para realizar cálculos digitales con cotas garantizadas sobre los errores de todas las fuentes.
• Puede ser utilizada para resolver problemas no lineales, como la solución a sistemas de ecuaciones no lineales y la programación no lineal.
 El redondeo y la estabilidad con aritmética de intervalo requieren especial atención. Cuando se realiza la aritmética en una computadora digital, es necesario tratar con los errores inducidos por redondeo de una manera dirigida. El redondeo hacia abajo de un número x es el menor número representable por la máquina que sea mayor o igual a x, y el redondeo hacia arriba convierte a x en el mayor número representable por la máquina que sea menor o igual a x. Uno de los problemas es que un algoritmo iterativo puede ser inestable, es decir, el intervalo puede crecer demasiado. Éste es uno de los principales inconvenientes.
El redondeo y la estabilidad con aritmética de intervalo requieren especial atención. Cuando se realiza la aritmética en una computadora digital, es necesario tratar con los errores inducidos por redondeo de una manera dirigida. El redondeo hacia abajo de un número x es el menor número representable por la máquina que sea mayor o igual a x, y el redondeo hacia arriba convierte a x en el mayor número representable por la máquina que sea menor o igual a x. Uno de los problemas es que un algoritmo iterativo puede ser inestable, es decir, el intervalo puede crecer demasiado. Éste es uno de los principales inconvenientes.
Existen varios esfuerzos por codificar subprogramas de cómputo para la aritmética de intervalos. Uno de los más completos, escrito por Yohe (1979), incluye todas las funciones propias del FORTRAN ANSI. Sin embargo, el número máximo de dígitos en que pueden ser representados los intervalos está limitado por el tamaño de las variables de tipo REAL, lo que en una arquitectura de 32 bits y representación IEEE-S754 significa un intervalo de operación entre ±10-4485 y ±1038.53.
También existe el trabajo de Jansen y Weidner (1986), quienes introdujeron el software ACRITH, diseñado en FORTRAN-77, y que cuenta con subrutinas para la inversión de matrices, cálculo de valores propios y cálculo de la raíz de un polinomio. Los métodos de redondeo utilizados son el redondeo hacia arriba, hacia abajo, más cercano y a cero. Las desventajas son que no puede combinarse con otros subprogramas para el manejo de precisión múltiple. Además, la parte medular del código está escrito en ensamblador para una arquitectura IBM/370, la cual es obsoleta.
El código INTLIB, publicado por Kearfott (1994), está escrito en FORTRAN-77 y su diseño está acorde a la filosofía de los subprogramas de álgebra lineal de código abierto BLAS (Basic Linear Algebra Subprograms), lo cual le permite su utilización conjunta: una poderosa opción. Desafortunadamente, su precisión queda reducida a la aritmética de punto flotante de doble precisión. Como punto favorable está su interfase FORTRAN-90, que permite definir las variables de manera intrínseca y sobrecargar las funciones aritméticas a los operadores convencionales.
 Algunos compiladores de FORTRAN-95, como el de SUN, ya proporcionan aritmética de intervalos como una extensión propia. Por otro lado, el centro de investigación INRIA en Francia ha desarrollado la biblioteca MPFI que permite utilizar aritmética de intervalos en base a GMP y está disponible de manera libre para su inclusión en código FORTRAN y C++: (http://pauillac.inria.fr/cdrom/prog/unix/mpfi/fra.htm).
Algunos compiladores de FORTRAN-95, como el de SUN, ya proporcionan aritmética de intervalos como una extensión propia. Por otro lado, el centro de investigación INRIA en Francia ha desarrollado la biblioteca MPFI que permite utilizar aritmética de intervalos en base a GMP y está disponible de manera libre para su inclusión en código FORTRAN y C++: (http://pauillac.inria.fr/cdrom/prog/unix/mpfi/fra.htm).
Los rangos
La aritmética de rangos conjunta las técnicas anteriores combinando la aritmética de intervalos con la precisión múltiple. De esta manera se maneja en memoria únicamente la precisión que el intervalo requiere, haciendo más eficiente el procesamiento y optimizando los recursos de cómputo.
Jones (1984) propuso un sistema para hacer aritmética de rangos. En su propuesta utiliza un formato de precisión múltiple para evitar los errores por truncamiento. Se almacenan valores para definir el límite superior e inferior de precisión, manteniendo restringida la precisión de la amplitud del intervalo. Definiendo una regla de significancia, basada en la preservación de la precisión sobre la amplitud del intervalo, se eliminan los dígitos no significativos después de cada operación, acotando así el crecimiento en el número de cifras conforme avanza el cálculo. Mediante las reglas de significancia, Jones demostró que con un número modesto de dígitos de guardia se puede garantizar una tasa baja de pérdida de precisión. Y aunque los resultados expuestos por Jones son significativos y prometedores, no existe desde su publicación un esfuerzo por codificar las rutinas que hiciera uso de las reglas de significancia.
El esfuerzo más cercano está en el trabajo de Aberth y Schaefer (1992). Codificaron una biblioteca en C++ para la aritmética de rangos, pero que carece de las reglas de significancia necesarias para evitar la pérdida de precisión. Por ejemplo, se guarda el valor del intervalo como un solo número, lo cual es un error.
Para el programador científico que se interesara por la utilización de rangos, sería conveniente revisar el código de Aberth y Schaefer para introducirle las reglas de significancia de Jones.
En fechas recientes se ha notado un renacimiento en la utilización de aritmética de rangos. Este interés se debe en parte a la mejora sustancial en poder de procesamiento y la creciente necesidad de cálculos más precisos. Por ejemplo, para sistemas de procesamiento de señales de punto flotante realizado en el 2003 por Fang y colaboradores (2003), o el dimensionamiento de circuitos analógicos por Lemke y colaboradores (2002).
Conclusiones
En algunos casos quizá no sea necesario aplicar uno de los métodos descritos con anterioridad. Puede ser suficiente pensar en binario, lo cual no es difícil. Sólo hay que recordar el sistema inglés de medición: la pulgada no se divide en décimas, sino que se divide en fracciones, todas potencias de 2, tales como 1/2, 1/4, 1/8, 1/16, 1/32, 1/64. Al dividir un intervalo o un área, o asignar valores para un incremento, esta forma de fraccionar la unidad es digitalmente más exacta que la división decimal.
Los programas que extienden la precisión requieren de mayor tiempo de cómputo. Pero el avance en la velocidad de procesamiento y las posibilidades de realizar cómputo en paralelo auguran que su utilización en el futuro será cada vez mayor. Para estar a la vanguardia en el desarrollo de programas de cómputo hay que saber cómo extender la precisión y fiabilidad de los resultados computacionales.
Hay gran cantidad de líneas de código fuente ya escritas que el investigador puede usar para desarrollar sus propios programas, y así dedicar sus esfuerzos a esa característica o idea única que marca el trabajo como propio. Cuando se quiere ver más lejos conviene, como hizo Newton, pararse sobre los hombros de gigantes.
Bibliografía
Aberth, O., y M. J. Schaefer (1992), "Precise Computation Using Range Arithmetic, via C++", ACM Trans. Math. Soft., 18, 481-491.
Bailey, D. H. (1995), "A FORTRAN-90 Based Multiprecision System", ACM Trans. Math. Soft., 21, 379-387.
Brent, R. P. (1978), "A FORTRAN Multiple-Precision Arithmetic Package", ACM Trans. Math. Soft., 4, 57-70.
Fang, C. F., T. Chen y R. A. Rutenbar (2003), "Floatingpoint Error Analysis Based on Affine Arithmetic", http://amp.ece.cmu.edu/Publication/Fang/icassp2003-fang.pdf.
Jansen, P., y Weidner P. (1978), "High Accuracy arithmetic Software —Some Tests of the ACRITH Problem-Solving Routines", ACM Trans. Math. Soft., 12, 62-70.
Jones, C. B. (1984), "A Significance Rule for Multiple-Precision Arithmetic", ACM Trans. Math. Soft., 10, 97-107.
Kearfott, R. B., M. Dawnde, K. Du y C. Hu (1978), "Algorithm 737: INTLIB: A Portable FORTRAN-77 Interval Standard-Function Library", ACM Trans. Math. Soft., 20, 447-459.
Knuth, D. E. (1981), The Art of Computer Programming, Vol.2: Seminumerical Algorithms, segunda edición, Addisson-Wesley.
Lemke, A., y L. Hedrich, y E. Barke (2002), "Analog Circuit Sizing Based on Formal Methods Using Affine Arithmetic", http://www.sigda.org/Archives/Proceedings Archives/llcad/llcad2002/07c\_1.pdf.
Smith, D. A. (1991), "Algorithm 693: A FORTRAN Package for Floating Point Multiple-Precision Arithmetic", ACM Trans. Math. Soft., 17, 273-283.
Smith, D. A. (1998), "Algorithm 786: Multiple-Precision Complex Arithmetic and Functions", ACM Trans. Math. Soft., 24, 358-367.
Miller, W. (1975), "Software for Roundoff Analysis", ACM Trans. Math. Soft., 1, 108-128.
Yohe, J. M. (1979), "Software for Interval Arithmetic: A Reasonably Portable Package", ACM Trans. Math. Soft., 5, 50-63.
Edscott Wilson García es maestro en matemáticas, graduado en la Universidad Autónoma Metropolitana y desde 1989 realiza tareas de investigación en el Instituto Mexicano del Petróleo (imp). Actualmente realiza estudios de doctorado en el Centro de Investigación y Estudios Avanzados (Cinvestav) del Instituto Politécnico Nacional gracias al apoyo del programa de becas del mismo Instituto. Esta dirección de correo electrónico está siendo protegida contra los robots de spam. Necesita tener JavaScript habilitado para poder verlo.
Guillermo Morales-Luna es doctor en ciencias matemáticas graduado del Instituto de Matemáticas de la Academia Polaca de Ciencias, y desde 1985 profesor de tiempo completo de la sección de computación del Cinvestav. Sus áreas de interés son teoría de la complejidad y lógica matemática. Esta dirección de correo electrónico está siendo protegida contra los robots de spam. Necesita tener JavaScript habilitado para poder verlo.
Pinzas ópticas: las delicadas manos de la luz
Pinzas ópticas: las delicadas manos de la luz
Karen Volke Sepúlveda, Ibis Ricárdez Vargas y Rubén Ramos García
![]()
Uno de los elementos más socorridos en las historias de ciencia ficción en las últimas décadas ha sido el láser. Y su fama es bastante bien merecida, ya que gracias a este dispositivo tan atractivo y estimulante para la imaginación de escritores y guionistas, la ciencia ha expandido sus fronteras, y las aplicaciones reales del láser se parecen cada vez más a las historias de ficción. Específicamente, una de sus aplicaciones más sorprendentes en los últimos años es la captura y manipulación de partículas microscópicas por medio de luz. Para entender en qué consiste esto, comencemos haciendo un breve recorrido histórico.
Los inicios de la captura óptica de partículas
Los primeros antecedentes que permitieron reconocer que la luz ejerce presión sobre los objetos materiales datan del siglo XVII, cuando Johannes Kepler (1571-1630) sugirió que la cola de los cometas podía deberse a la presión de los rayos solares, ya que siempre apuntaba en sentido contrario al Sol sin importar la dirección de movimiento del cometa (aunque en realidad esto se debe al viento solar, ya que la presión de radiación de la luz solar no es lo suficientemente fuerte como para desviar la cola de los cometas). Más de dos siglos después James Clerk Maxwell (1831-1879) desarrolló su teoría electromagnética, con la cual demostró que la luz está constituida por ondas electromagnéticas que efectivamente ejercen presión al propagarse. Algunas décadas más tarde se observaron fenómenos que no podían explicarse con la teoría ondulatoria de Maxwell, lo cual dio lugar a los inicios de una de las grandes teorías del siglo XX: la mecánica cuántica. En este contexto, los trabajos principalmente de Albert Einstein (1879-1955) y Max Planck (1858-1947) llevaron a la conclusión de que, bajo ciertas circunstancias, la luz también se comporta como si estuviera formada por un flujo de partículas, actualmente llamadas fotones. A cada fotón se le asocia una propiedad llamada momento lineal (que en física clásica se define como el producto de la masa por la velocidad de un cuerpo, aunque según la teoría de la relatividad, aun una partícula sin masa, como el fotón, puede tener momento lineal, cuya magnitud es igual a su energía dividida por la velocidad de la luz). Esto se traduce en el hecho de que el flujo de fotones en su conjunto ejerce presión al incidir sobre la materia. Es decir, independientemente del comportamiento específico de la luz (ondulatorio o corpuscular), se reconoce que ésta es portadora tanto de energía como de momento lineal, y ambas cantidades se conservan en cualquier proceso de interacción entre radiación y materia.

Como es natural, hubo muchos intentos en el siglo XX de medir la presión ejercida por la luz, pero ésta es en general demasiado débil (por ejemplo, la presión de la radiación solar en la superficie terrestre equivale aproximadamente a 10-11 de la presión atmosférica -es decir, es 0.00000000001 veces menor que la presión atmosférica). Se requería de un extraordinario refinamiento en las técnicas y equipos experimentales, así como fuentes luminosas adecuadas, para detectarla.
La historia cambió radicalmente cuando el láser apareció en escena, en los años sesenta. ¿Qué hace del láser una fuente de radiación tan especial? Por una parte, el hecho de que la radiación que emite es casi monocromática y coherente. Esto quiere decir que está formada por un conjunto de ondas electromagnéticas que tienen casi todas la misma longitud de onda (es luz de un solo color) y que viajan de manera ordenada y sincronizada. Por otra parte, la luz del láser concentra una gran potencia, y se propaga a lo largo de una dirección bien definida (como rayo). En óptica nos referimos a este tipo de propagación como un haz de luz. Por ejemplo, si enfocamos un haz de luz láser de 1 watt de potencia a una superficie de unos 10 micrómetros (milésimas de milímetro) de diámetro, la cantidad de fotones que atravesarán esa superficie por unidad de tiempo será más de nueve millones de veces mayor que la cantidad de fotones que la atravesarían si la misma superficie estuviera iluminada por el Sol en el exterior de la atmósfera terrestre. En este caso, la presión de radiación sigue siendo insignificante para objetos macroscópicos, pero llega a ser muy importante al actuar sobre objetos suficientemente pequeños.
Con base en este tipo de argumentos, en 1970 Arthur Ashkin, científico norteamericano que trabajaba en los laboratorios Bell en Estados Unidos, diseñó un experimento para medir la presión de radiación ejercida por un láser continuo. Para evitar efectos de calentamiento debidos a la absorción de la luz, Ashkin utilizó microesferas transparentes de látex suspendidas en agua, cuyos diámetros iban desde fracciones de micrómetro hasta varios micrómetros (como comparación, el grosor de un cabello humano es aproximadamente de 50 a 150 micrómetros). Para su grata sorpresa, no sólo encontró que la presión de radiación efectivamente era capaz de empujar a las partículas en la dirección de propagación del haz láser, sino que también observó que, simultáneamente, las partículas eran atraídas hacia el centro del haz, en la dirección transversal. Partiendo de estos resultados Ashkin decidió colocar dos haces de luz propagándose en direcciones opuestas a lo largo de un eje horizontal, de modo que las fuerzas ejercidas por cada uno de los láseres se equilibraran entre sí en algún punto intermedio, donde la partícula quedaría atrapada por la luz. Estos descubrimientos marcaron el inicio de lo que hoy en día se ha convertido en una de las áreas de mayor impacto en la ciencia y la tecnología: la micromanipulación óptica.
El origen de las fuerzas de captura óptica
Para entender el fenómeno observado por Ashkin recurriremos a la Figura 1, donde el proceso de interacción entre la luz y una partícula esférica se ilustra mediante un trazo de rayos. Cuando un haz de luz incide sobre la superficie de un objeto transparente, una parte de la luz es reflejada; otra parte es transmitida (pasa a través del objeto), pero sufre refracción (se desvía), y puede haber también una pequeña parte que se absorba, transformándose en calor. Los cambios en la rapidez o dirección de propagación de la luz debidos a la reflexión y refracción implican un cambio en el momento lineal de los fotones, lo cual a su vez genera fuerzas que actúan sobre la partícula; esto se debe a que el momento lineal se debe conservar, y ocasiona la presión de radiación.
Pero hay un ingrediente adicional que permite la captura óptica observada por Ashkin, y es el hecho de que existe un gradiente de intensidad en la sección transversal del haz de luz: la intensidad es máxima en el centro y disminuye rápidamente hacia las orillas, como se ilustra en la Figura 1a y en la curva roja de las Figuras 1b y c (por lo cual el rayo a se representa un poco más grueso que el rayo b). La refracción del rayo a en la figura 1b provoca la fuerza Fa sobre la esfera, y el rayo b, simétricamente ubicado, causa una fuerza análoga Fb, pero Fa es mayor que Fb. El resultado es que la fuerza total (flecha azul) tiene dos contribuciones; una perpendicular al eje de propagación (z) que conduce las partículas hacia las regiones de máxima intensidad; y la otra que las empuja hacia adelante a lo largo del eje. La primera se conoce como fuerza de gradiente, mientras que la segunda se ha llamado fuerza de esparcimiento o dispersión.
En el caso de la luz reflejada (Figura 1c), la fuerza ejercida en cada punto del objeto es siempre perpendicular a su superficie (debido a la ley de reflexión de la luz), de manera que la fuerza resultante tiene el efecto principal de empujar al objeto en la dirección de propagación (flecha azul). Sin embargo, el gradiente de intensidad también juega un papel en este caso. De hecho, su efecto es exactamente opuesto al de la fuerza gradiente para la luz transmitida, es decir, tiende a empujar al objeto fuera de las regiones de intensidad máxima, aunque su magnitud es mucho menor (aproximadamente diez veces) que la fuerza gradiente asociada a la luz transmitida. En general, podemos decir que la fuerza de esparcimiento es aquella cuya dirección coincide siempre con la dirección de propagación del haz de luz, mientras que la fuerza gradiente es perpendicular a esta dirección.
En la década de los setenta y principios de los ochenta, tanto Ashkin y su equipo de colaboradores como otros grupos científicos alrededor del mundo centraron su atención en comprender mejor los fundamentos físicos del fenómeno y en desarrollar nuevas técnicas de captura óptica. Por ejemplo, se realizaron diversos experimentos de "levitación óptica" con partículas micrométricas de diferentes materiales y propiedades ópticas (partículas transparentes de alto y bajo índice de refracción, partículas metálicas, etcétera). La levitación se obtiene cuando la presión de radiación ejercida por un haz de luz que se propaga verticalmente hacia arriba, equilibra a la fuerza de gravedad de tal manera que la partícula queda suspendida.
A pesar de estos avances, las aplicaciones de las técnicas de captura óptica aún se veían bastante limitadas. Sin embargo, en 1986 se obtuvo otro gran avance en el área, nuevamente debido a Ashkin y a sus colaboradores, entre los que destaca Steven Chu, premio Nobel de física 1997 por sus contribuciones al enfriamiento y captura de átomos con luz. Esta vez desarrollaron una "trampa óptica" muy estable, que permitía atrapar firmemente a una partícula utilizando un solo haz de luz. Para lograr esto, el haz se debe enfocar en un área extremadamente pequeña utilizando una lente objetivo de microscopio (de manera análoga a como se enfoca la luz del Sol mediante una lupa). Con ello se genera un considerable gradiente de intensidad en la dirección de propagación, además del transversal. Como consecuencia, la fuerza de gradiente atrae a las partículas hacia la región focal, donde la intensidad es máxima. Lo sorprendente es que esta fuerza tiene magnitud suficiente como para equilibrar el peso de la partícula y la fuerza de esparcimiento, de modo que las partículas pueden ser atrapadas aun cuando el haz se dirija verticalmente hacia abajo. Este tipo de trampa se conoce hoy en día como "pinzas ópticas", y su eficacia se ha comprobado con partículas cuyos tamaños van desde decenas de nanómetros (millonésimas de milímetro) hasta decenas de micrómetros (milésimas de milímetro). El principio de operación en este caso se ilustra en la Figura 1d. Las fuerzas ejercidas por los rayos a y b sobre la esfera corresponden a Fa y Fb, respectivamente, y la fuerza total apunta en dirección del plano focal (flecha azul).
El método ilustrado en las figuras 1b-d describe satisfactoriamente las fuerzas ópticas sólo cuando el tamaño de las partículas es varias veces mayor que la longitud de onda de la luz que se está utilizando. También se pueden atrapar partículas más pequeñas, pero los procesos físicos involucrados y su descripción son más complejos. En general, las fuerzas ópticas son directa mente proporcionales a la potencia del haz de luz. Aunque la potencia mínima necesaria para atrapar una partícula depende de su tamaño, de sus propiedades ópticas y, por supuesto, de las demás fuerzas involucradas en el sistema, generalmente unos cuantos miliwatts pueden ser suficientes.

Figura 1. (a) Gradiente de intensidad transversal de un haz de luz láser y su proyección en una pantalla. (b-d) Procesos de interacción entre un haz de luz y una partícula: (b) El gradiente de intensidad provoca una fuerza neta que atrae a la partícula hacia la región más intensa, a tiempo que la empuja en la dirección de propagación. (c) La fuerza asociada a la luz reflejada se dirige principalmente en la dirección de propagación. (d) Si el haz de luz está muy enfocado, se genera un gradiente de intensidad a lo largo del eje del haz que provoca que la partícula sea atraída hacia el plano focal, que es la región de mayor intensidad.
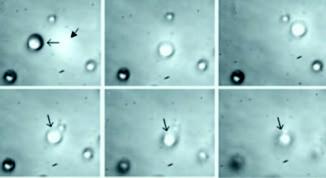
Una vez que una partícula está atrapada se puede desplazar con respecto a su entorno, ya sea moviendo el haz de luz o la propia muestra que contiene a la partícula; en este caso se habla de "manipulación óptica". Otro punto importante es que estas técnicas no están restringidas a partículas esféricas: funcionan igualmente con objetos de diferentes geometrías, e incluso de formas irregulares, aunque en esos casos puede haber efectos adicionales de alineación o rotación. En la Figura 2 se muestra una secuencia de imágenes que permite apreciar la manipulación de una pequeña esfera de vidrio en las tres direcciones espaciales.
El impacto de las pinzas ópticas fue determinante en el desarrollo posterior de las técnicas de manipulación con luz, y los resultados más emocionantes aún estaban por venir. Hasta 1986 los experimentos se habían realizado con luz visible (con longitud de onda aproximadamente de 0.40 a 0.70 micrómetros). El grupo de Ashkin había utilizado un láser de luz verde con una longitud de onda de 0.514 micrómetros. En 1987, una afortunada casualidad y su gran ingenio los condujeron a otro descubrimiento fundamental. Al realizar un experimento en el que pretendían manipular cierto tipo de virus, de pronto observaron que algunos especímenes que no eran virus caían en la trampa óptica, se movían frenéticamente por unos momentos y después quedaban inmóviles, capturados por la luz. Al analizarlos se dieron cuenta de que la muestra había sido contaminada por bacterias que, al ser atrapadas, morían rápidamente a causa de la fuerte absorción de radiación.
|
Figura 2. Manipulación en tres dimensiones de una esfera de vidrio de 5 micrómetros suspendida en agua. (a) Se observa la imagen transversal del haz de luz proyectada en el plano de la muestra; (b) el haz se ha dirigido hacia una partícula atrapándola; en (c) se puede ver cómo ésta se ha desplazado lateralmente a otra posición respecto a sus vecinas. En las imágenes (d-f) la partícula señalada con la flecha es la que está atrapada y el resto de las microesferas se desenfocan, lo cual indica que la partícula atrapada se está desplazando en la dirección vertical. |
Entonces se les ocurrió reemplazar la luz verde por un láser infrarrojo (con longitud de onda de 1.064 micrómetros), ya que la radiación infrarroja prácticamente no es absorbida por la materia biológica y por lo tanto no le causa daño. Los resultados fueron extraordinarios; no sólo lograron atrapar y manipular bacterias, levaduras (hongos microscópicos) y diferentes tipos de células vivas, sino que además las pudieron mantener en la trampa el tiempo suficiente como para observar la reproducción celular sin que sufrieran daño. Incluso se logró la manipulación de organelos celulares dentro de algunos tipos de células in vivo, lo que permitió estudiar la estructura interna de la célula en cuestión.
Por otra parte, hasta ese momento se habían utilizado dos microscopios en el montaje experimental; uno para enfocar el haz láser y otro para observar las partículas atrapadas. Pero en el mismo trabajo de 1987 se reporta por primera vez la combinación del sistema de focalización con el sistema de observación en un solo objetivo de microscopio, que desempeñaba ambas funciones. Una configuración experimental muy simple pero típica de estas pinzas ópticas modernas se describe en la Figura 3, aunque hoy en día se utilizan muchas configuraciones diferentes, dependiendo de la aplicación; inclusive se pueden realizar introduciendo el láser directamente a un microscopio óptico.

Figura 3. Un arreglo experimental simple de pinzas ópticas. El láser (L) se dirige mediante un conjunto de espejos hacia el objetivo de microscopio que se utilizará para enfocarlo. El último espejo (E) es selectivo, de manera que refleja la luz del láser pero permite observar la muestra a través de la iluminación de fondo (F) y un sistema de detección (D), que típicamente consiste de una cámara. La muestra se encuentra sobre una base de traslación que permite su movimiento relativo al haz de luz.
Aplicaciones sobresalientes y nuevos avances
La manipulación de muestras biológicas y la simplificación del sistema experimental abrieron de manera definitiva la gama de aplicaciones de las pinzas ópticas. Actualmente se han convertido en una herramienta fundamental en disciplinas como biofísica, biotecnología, medicina reproductiva y biología celular y molecular, donde han hecho posible la manipulación incluso de una sola molécula. También se usan en investigaciones básicas en óptica, para determinar las propiedades físicas de diferentes tipos de haces de luz, así como en estudios de física de coloides (materiales de tipo gelatinoso) y sistemas complejos. Por si eso fuera poco, las nuevas técnicas de manipulación óptica permiten la operación de máquinas en miniatura, que, dicho sea de paso, son también desarrolladas con tecnología óptica. Un ejemplo de gran interés en el terreno de las aplicaciones biológicas es el estiramiento de una sola molécula de ácido desoxirribonucleico (ADN, que normalmente se mantiene en una configuración enrollada), lo cual ha sido fundamental para entender sus propiedades mecánicas y por tanto sus funciones en la operación de la maquinaria celular. Una manera de lograr esto es adherir uno de los extremos de la molécula (previamente marcada con un material fluorescente y detectado mediante microscopía de fluorescencia) a una esfera de látex que es atrapada con pinzas ópticas. Posteriormente se utiliza la fuerza hidrodinámica de un líquido que fluye para estirar la molécula de ADN (¡hasta una longitud de 64.5 micrómetros!). Cuando el flujo se detiene, la molécula se relaja volviendo a su forma original.
También se ha combinado el uso de las pinzas ópticas con lo que se conoce como "escalpelo óptico" para realizar fertilización in vitro. El escalpelo óptico consiste básicamente en enviar un pulso corto y controlado de luz láser de muy alta energía y longitud de onda ultravioleta (menor de 0.40 micrómetros) que "taladra" un agujero en la zona pelúcida de un óvulo (la capa protectora que lo rodea) con gran precisión, para facilitar la llegada del espermatozoide, el cual a su vez es arrastrado hasta el óvulo utilizando pinzas ópticas. El escalpelo óptico es también una herramienta muy poderosa, que permite entre muchas otras cosas, aislar células individuales de un tejido sano o enfermo para estudiar las diferencias a nivel molecular.

Otro ejemplo impresionante es el estudio de los procesos de transporte por motores molecular es (enzimas especiales, como la kinesina, que catalizan algunas reacciones químicas en el interior de la célula y utilizan la energía liberada para realizar trabajo mecánico, como el transporte de cromosomas a través del citoplasma, que los arrastra a lo largo de los filamentos proteicos llamados microtúbulos). La molécula de kinesina se compone de dos cadenas pesadas entrelazadas, lo que le da una forma alargada, y uno de sus extremos funciona como un par de "piernas" con las que recorre su camino. En este caso, un extremo de la kinesina se adhiere a una esfera transparente atrapada con luz; conforme la kinesina se empieza a desplazar a lo largo de un microtúbulo, es capaz de arrastrar consigo a la esfera. Caracterizando el desplazamiento de la esfera respecto a su posición inicial de equilibrio en la trampa óptica se logra caracterizar el movimiento de la kinesina. Con estas investigaciones se han comenzado a develar los misterios de la kinesina, concluyendo que ésta se mueve con pasos regulares de aproximadamente 8 nanómetros de longitud.
Los ejemplos anteriores involucran el uso de las formas más simples de las pinzas ópticas. Pero las posibilidades de manipulación óptica son cada vez más amplias, y hoy se cuenta con nuevas técnicas desarrolladas en la última década. Tal es el caso de las trampas ópticas que involucran el uso de haces con distribuciones controladas de luz, como arreglos de regiones brillantes y oscuras que actúan como trampas individuales, permitiendo la manipulación de múltiples objetos a la vez. En las imágenes a-c de la Figura 4 se muestran simulaciones numéricas de algunas distribuciones de intensidad que se han utilizado para manipulación, mientras que en los cuadros d-f se muestran imágenes de los experimentos correspondientes.
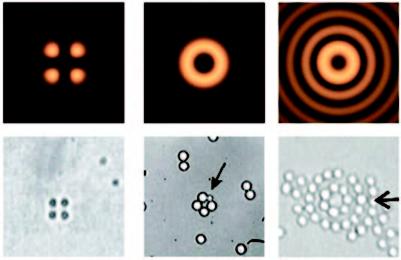
Figura 4. (a) Algunas distribuciones transversales de intensidad generadas con diferentes técnicas ópticas y (b) su correspondiente aplicación en la captura óptica de macropartículas, donde se puede observar que las partículas se acomodan de acuerdo con la distribución de intensidad de cada haz.
Una manera de cambiar y controlar la distribución transversal de intensidad de un haz de luz es utilizan-do técnicas de interferencia; es decir, dividiendo un haz de luz en dos y recombinándolo más adelante de modo que la energía se redistribuya formando regiones brillantes y oscuras.
Otra forma de moldear un haz de luz es utilizando hologramas generados por computadora. Los hologramas son básicamente rejillas de difracción (formadas, por ejemplo, por variaciones espaciales de absorción, de espesor o de índice de refracción, con escalas de longitud semejantes a la longitud de onda de la luz) con ciertas deformaciones en su estructura que codifican la información necesaria para lograr que la luz que las atraviesa se redistribuya de acuerdo a una configuración deseada. Más aún, en la actualidad existen ciertos dispositivos llamados moduladores espaciales de luz, que podríamos describir como pequeñas pantallas de cristal líquido que se conectan directamente a una computadora, en las cuales se despliega la configuración gráfica correspondiente al holograma (como una copia a escala de lo que se ve en el monitor de la computadora. Así, un modulador espacial al ser atravesado por la luz actúa del mismo modo en que lo hace un holograma convencional, pero con la gran ventaja de que puede reconfigurarse de manera interactiva, lo cual se conoce como holografía dinámica. En el terreno de las pinzas ópticas, las posibilidades de controlar la distribución transversal de intensidad del láser permiten manipular varias partículas simultáneamente, de acuerdo con secuencias específicas (en algunas de las páginas web recomendadas al final de este artículo se pueden ver videos de este tipo de trampas dinámicas). Esto ha dado un nuevo y brillante potencial a las aplicaciones de las pinzas ópticas. Por ejemplo, además de la traslación en cualquier dirección, se ha logrado también la rotación controlada de los objetos microscópicos atrapados, lo cual ya se está aplicando como mecanismo para manejar elementos de micromáquinas.
Es tan amplio el espectro de aplicaciones de las pinzas ópticas que resulta imposible resumirlo. Nuestro propósito aquí ha sido simplemente motivar al lector interesado en el tema, tratando de dar un panorama muy general.
Agradecimientos
Los autores agradecen sus valiosos comentarios a Shahen Hacyan y a Eugenio Ley Koo. K. V. S. agradece a la DGAPA-UNAM por su apoyo a través del proyecto IN103103.
Karen Volke Sepúlveda estudió la licenciatura en física en la Universidad Nacional Autónoma de México (UNAM). Obtuvo la maestría y doctorado en ciencias en el Instituto Nacional de Astrofísica, Óptica y Electrónica (inaoe), en la especialidad de óptica. Su tesis doctoral fue galardonada con el premio Weizmann a la mejor tesis doctoral en el área de ciencias exactas en 2003. También en 2003 recibió el Premio Europeo de Óptica por una de sus publicaciones. Es miembro del Sistema Nacional de Investigadores y es investigadora titular del Instituto de Física de la UNAM en el tema de micromanipulación óptica y propiedades dinámicas de haces de luz. Esta dirección de correo electrónico está siendo protegida contra los robots de spam. Necesita tener JavaScript habilitado para poder verlo.
Ibis Ricárdez Vargas es físico por la Universidad Juárez Autónoma de Tabasco. Obtuvo una maestría en ciencias con especialidad en óptica en el INAOE, en donde actualmente es estudiante de doctorado en el tema de pinzas ópticas. Esta dirección de correo electrónico está siendo protegida contra los robots de spam. Necesita tener JavaScript habilitado para poder verlo.
Rubén Ramos García obtuvo el doctorado en física en el Imperial College of Science, Technology and Medicine de Londres. Es investigador titular del INAOE y miembro del Sistema Nacional de Investigadores. Sus áreas de interés son materiales fotorrefractivos (polímeros, pozos cuánticos y cristales en volúmenes), materiales orgánicos no lineales, aplicaciones de materiales fotorrefractivos y micromanipulación óptica. Esta dirección de correo electrónico está siendo protegida contra los robots de spam. Necesita tener JavaScript habilitado para poder verlo.
Bibliografía
Ashkin, A. (1999), "Optical trapping and manipulation
of neutral particles using lasers", Optics and Photonics
News, 10, 41-46. Bustamante, C., Z. Bryant y S. B. Smith (2003), "Ten years
of tension: single molecule DNA mechanics," Nature,
423-427. Dholakia, K., G. Spalding y M. P. MacDonald (2002),
"Optical tweezers: the next generation", Physics World,
15, 31-35. Hecht, Eugene (2000), Óptica, 3s edición, Madrid,
Addison-Wesley, pp. 2-10, 55-57.
Molloy, J. E. y M. J. Padgett (2002), "Lights, action: optical tweezers", Contemporary physics, 43, 241-258. Prasad, Paras (2003), Introduction to Biophotonics, Wiley
Interscience, pp. 482-519. Rubinsztein-Dunlop, H., y M. Friese (2002), "Light-driven
micromachines", Optics and Photonics News, 13, 22-26.
Algunas páginas web recomendadas
Grupo de atrapamiento óptico de la Universidad de St.Andrews, www.st-andrews.ac.uk/~atomtrap/;
Grupo de Óptica de la Universidad de Glasgow, www.physics.gla.ac.uk/Optics/;
Micromáquinas complejas producidas e impulsadas por luz, www.zbk.uszeged.hu/%7Egpeter/micromachine/micromachine.htm;
Estudios de manipulación de moléculas individuales, Universidad de California en Berkeley, http://alice.berkeley.edu/;
Óptica de fase programable, Laboratorio Nacional Risø, Dinamarca, www.risoe.dk/ofd/ppo/PPOG_mbot.htm;
Atrapamiento óptico holográfico, Universidad de Nueva York, http://physics.nyu.edu/grierlab/hot/index.shtml;
Laboratorio BLOCK, Universidad de Stanford, www.stanford.edu/group/blocklab
La codificación de los quipus incas
Hugo Cabrera Ibarra, Haret C. Rosu Barbus, Luis A. Torres González, J. Pablo Treviño Gutiérrez
![]()
Introducción
Aproximadamente en el periodo de 1400 a 1532, el pueblo inca registraba datos importantes de una manera peculiar: haciendo uso de cordeles de algodón u, ocasionalmente, de fibras de animales como la llama o vicuña. Estos objetos, que poseían nudos de diferentes formas y colores, estaban sujetos a una cuerda principal, y toda esta estructura textil se conocía como quipu.
A diferencia de los pueblos mesoamericanos, donde se tienen documentos históricos en forma de códices, en la zona andina son los quipus, las telas que envolvían a las momias, las que se colgaban en los edificios de importancia, las ropas de los jefes, la cerámica y ciertos pequeños frijoles los que contienen la información socioeconómica, así como los conocimientos, tradiciones y relatos religiosos. Los quipus, además, registran fechas y acontecimientos sobresalientes, que no debían olvidarse.
El registro de datos era numérico y se cree que también literario. El primer código ha sido descifrado; sin embargo, el segundo permanece como un enigma, pues los incas no contaban con un sistema de escritura. Se sabe que en Cuzco se tenían datos exactos acerca de la cantidad de personas, sus edades y sexo en las diferentes provincias; a partir de esta observación se pudo apreciar una de las utilidades de los quipus como dispositivos de conteo. Todo indica también que a partir de los quipus los incas conocían el sistema decimal gracias al sistema de nudos, sus colores y sus tamaños.
Un poco de historia
El imperio inca se extendió desde el Ecuador hasta la región central de Chile (véase mapa). El corazón del imperio estaba en Cuzco, en la zona andina del sur de Perú. Hacia 1532 la guerra entre dos hermanos y enemigos alcanzaba su máximo: los hijos de Huayna Capac, Atahualpa, instalado en Quito, y Huáscar, en Cuzco, se disputaban las tierras que su padre había dividido al momento de morir. Esta discordia entre hermanos precipitó la división del imperio inca y la caída de su civilización. Durante ese mismo año, el español Francisco Pizarro desembarcó en la ribera del Ecuador, con planes de conquista. Esto intensificó la debilidad del imperio inca, aunque el final de la conquista no se dio sino después de años de guerra con el último hijo de Huayna Capac, de nombre Manco Capac.
Varios años después, el historiador mestizo Garcilaso Inca de la Vega, conocido también como "El Inca", quien dominaba el idioma quechua local por ser uno de los primeros mestizos, viajó a lo largo del imperio con el fin de registrar por escrito las costumbres y tradiciones del territorio inca. El famoso cronista, nacido en Cuzco, era hijo natural del conquistador español Sebastián Garcilaso de la Vega y Vargas y de la "ñusta" (princesa, en quechua) inca Isabel Chimpo Ocllo. En la primera parte de su obra máxima, los Comentarios reales (1609), De la Vega trata la historia, cultura e instituciones sociales del imperio inca; en tanto que en la segunda, titulada Historia general del Perú (publicada póstumamente en 1617), se ocupa de la conquista de esas tierras y de las guerras civiles. Según la descripción de De la Vega, cuando los indígenas iban a Cuzco a pagar los tributos a los nuevos jefes llegados de Europa, traían una serie de cordeles de diferentes colores sobre los cuales escribían números con la ayuda de distintos nudos. Los cordeles eran ordenados, amarrados y suspendidos a lo largo de una cuerda principal (véase fotografía). Éste es el primer escrito que menciona a los quipus.
 .
.
Los quipus: ¿solo para contabilizar?
La palabra quipu significa "nudo" en quechua. Además del contenido numérico, se piensa que los quipus también tenían información literaria que aún permanece en espera de ser descifrada por el trabajo de investigación de los expertos. Algunos documentos coloniales indican que los quipus eran utilizados para archivar y contabilizar registros, así como para remitir información y mensajes por medio de correos (llamados chasques) a lo largo y ancho del imperio. 
A pesar de que en el imperio inca no se conocía ningún tipo de escritura convencional, su organización era catalogada de una manera detallada y metódica. ¿Será que los quipus también sirvieron para indicar una forma de escritura aún no entendida? Los quipus eran el único modo preciso de transportar información que tenía el pueblo inca: censos, situación de las reservas de producción agrícola, cantidad de productos de la minería, el número de trabajadores, etcétera. En otras palabras, estos dispositivos mantenían la información de los datos históricos, tratados de leyes, documentos de paz o guerra y demás. Los quipus, teniendo esta información, eran transportados por una red de rutas terrestres establecidas por mensajeros organizados en regiones y puntos específicos de todo el territorio imperial.
En esa época, solamente los quipucamayocos (guardianes del quipu) o administradores sabían el significado de los quipus. La mayoría de los quipus en Cuzco o en la provincia fueron destruidos por el ejército de Atahualpa, y más tarde por los oficiales del rey de España, obedeciendo la orden del virrey Francisco de Toledo, con el fin de eliminar la riqueza cultural del imperio inca. Los pocos ejemplares que se pueden admirar hoy en día en museos (alrededor de 600) fueron descubiertos en sitios funerarios, pues era costumbre de los incas sepultar a sus muertos junto con los objetos que utilizaron a lo largo de la vida.

Fotografía de un quipu.
Anatomía de un quipu ¿Cómo se codificaba la información numérica en un quipu? De la Vega es muy preciso en sus observaciones: un quipu está constituido por una cuerda gruesa llamada "principal", sobre la cual se amarran otras cuerdas pequeñas o cordeles de 20 a 50 centímetros de longitud. En un quipu puede haber hasta 2 mil cordeles. Al colocar un quipu sobre un plano horizontal (Figura 1) los cordeles tienen diferente orientación, algunos hacia arriba y otros hacia abajo. La mayoría de los cordeles presentan nudos; pero, ¿qué significan éstos? A pesar de los esfuerzos de los escritores españoles, el misterio de los quipus no podía comprenderse. No fue sino hasta 1912 que el norteamericano Leland Locke fue capaz de descifrar un quipu que se encontraba en el museo de historia natural de Nueva York (Figura 1).
 |
|
Figura 1. Dibujo de un quipu donde se representa la manera de codificar operaciones de suma. |
Locke usó las descripciones de De la Vega, donde se especificaba que los números codificados por los nudos dependían de la posición en la cual se encontraban sobre cada uno de los cordeles. Los cordeles de un quipu presentan tres grupos de nudos: un grupo inferior, que Locke interpretó como las unidades; un grupo central para las decenas, y un grupo cercano a la cuerda principal para las centenas. Esta hipótesis se confirmó cuando él notó que cada grupo de cordeles de abajo estaba enlazado por una cuerda de arriba cuyo valor, indicado por sus nudos, correspondía a la suma de los otros (Figura 1).
Tres tipos de nudos
De las interpretaciones de Locke se concluye que la codificación de los quipus es similar a nuestro sistema decimal (en base 10). Recordemos las principales características de este sistema: se dispone de 10 símbolos distintos, las cifras del 0 al 9. En un número como el 6139, cada cifra corresponde a la cantidad de una potencia n-ésima de 10, donde n varía desde 0 a la derecha, aumentando una unidad cada vez que se desplaza una posición hacia la izquierda. Por ejemplo, 6 139 = 6 x 103 + 1 x 102 + 3 x 101 + 9 x 10°, o bien, 6 139 = 6000 + 100 + 30 + 9. Nótese que el sistema posicional no está conectado con la base 10. Por ejemplo, los mayas contaban usando un sistema vigesimal, o sea con base 20, usando también un sistema posicional. En el caso de los quipus, las posiciones se consideran con respecto a la cuerda principal, siendo la posición más lejana la de potencia más baja. Por otro lado, los nudos sobre los cordeles son sólo de tres tipos diferentes, a diferencia de las diez cifras actuales (véase Figura 2). Los nudos simples corresponden a las potencias de 10, en los nudos largos un nudo simple en el cual se hacen varios enrollamientos antes de cerrarlo: en (a), cada vuelta es una unidad, b=2, c=5, d=8, y los nudos en forma de 8, que representa una sola unidad. Sobre un cordel los nudos se reparten en grupos de 1 a 9 nudos, así que están las nueve cifras excepto el 0. Cada grupo está afectado de una potencia de 10, que se incrementa al acercarse a la cuerda principal, excepto los grupos de las unidades, que son los únicos grupos de nudos largos y en donde se termina cada número. Sin embargo, cuando hay una sola unidad, el nudo largo de un solo enrollamiento se reduce a un nudo simple y se puede confundir con una potencia de 10. La manera de salir de esta situación ambigua provocada por las unidades aisladas fue, para los incas, hacer un nudo en forma de 8 para una sola unidad. Recuperando el ejemplo del número 6 139, se describe cómo sería su representación quipu: 6 139 = un grupo de 6 nudos simples, pegado a la cuerda principal; un nudo simple, un grupo de 3 nudos simples, un nudo largo de 9 enrollamientos.
Figura 2. Se muestran los tres tipos de nudos: largos (a partir de dos enrollamientos hasta nueve, a-d, en donde a es un nudo largo no apretado), simples (de potencias de 10, e), y en forma de ocho (para una sola unidad aislada, f).
Sobre las cuerdas, el 0 está indicado por la ausencia de nudo en un grupo. Las unidades son identificadas fácilmente por el tipo de nudo, mientras que los grupos de nudos están alineados en la misma posición sobre todas las cuerdas, de modo que se identifican con facilidad las posiciones sin nudos. Aún más: la falta de ambigüedad para las unidades que se agregan se puede observar en algunos casos, cuando se presentan varios números sobre la misma cuerda.

El desciframiento que hemos comentado se limita al aspecto numérico, y hasta ahora no ha sido contradictorio. En cambio, ¿qué se puede decir de la expresión de las ideas y de los hechos? En este asunto existe mucha polémica. De nuevo hay indicaciones en primera línea del mismo historiador De la Vega. Según él, se puede saber el significado extranumérico de los cordones a través de los colores que llevan. Hay cordones de un solo color, otros de dos, tres y más. Los colores simples y muchas de las combinaciones de los mismos tendrían su propio significado.
Hacia la interpretación del contenido extranumérico
Sobre algunos quipus también se pudo explicar la expresión de los recursos de armas de un pueblo: por ejemplo, las combinaciones de color de manera jerárquica, para las armas; sobre el primer cordel están las armas más nobles, como lanzas, dardos, arcos, flechas, hachas, escudos, etcétera.
El sentido de torsión de los hilos de las cuerdas podría tener también un significado. Vueltas hacia la derecha representan cosas positivas, y al contrario podrían tener un sentido negativo. Tal significado escondido en la torsión de los hilos daría solución al misterio de la ausencia de escritura. ¿Cómo era posible que una civilización con bastante complejidad y organización sobre un territorio tan extenso como casi la mitad de Sudamérica pudiera mantenerse sin escritura?
Gary Urton (2003), reconocido antropólogo de la Universidad de Harvard, ha propuesto la existencia de un código binario en los cordeles de quipu equivalente a una escritura. Se trata de un sistema completamente inédito, que todavía es objeto de debate, y radicalmente diferente de nuestro sistema de escritura. Según Urton, el significado de cada uno de los nudos sería obtenido de un conjunto de cuestionamientos, conocidos también como cadena operacional. ¿El nudo está hecho de lana del camélido denominado llama? ¿Una cuerda está arriba o abajo? ¿Los hilos son rojos o azules?
Por ejemplo, en lo que se refiere a los colores, Urton utilizó la simbología de colores que aún es usada por los tejedores bolivianos, quienes pueden distinguir 24 colores. En total, el antropólogo distinguió seis decisiones binarias y una elección múltiple (el color). Al final, el repertorio de un quipu tendrá un total de 26 x 24 = 1 536 signos de información distintos. Este repertorio es por tanto más amplio que el que posee la escritura cuneiforme de Mesopotamia, y también que el de los jeroglíficos egipcios.
 Urton ha presentado de manera informática todos los detalles de los quipus, de forma que los datos referidos a la codificación estén disponibles al público. En junio de 2003 Carrie Brezine, sastre y matemática, aportó una copia de los quipus encontrados en una caverna situada cerca del lago de los Cóndores, en el norte de Perú. Sobre tres de estos quipus se notaban largas series de nudos casi idénticos, mostrando que la información estaba copiada de unos a otros de la misma manera que los monjes copistas del medievo reproducían los manuscritos a mano.
Urton ha presentado de manera informática todos los detalles de los quipus, de forma que los datos referidos a la codificación estén disponibles al público. En junio de 2003 Carrie Brezine, sastre y matemática, aportó una copia de los quipus encontrados en una caverna situada cerca del lago de los Cóndores, en el norte de Perú. Sobre tres de estos quipus se notaban largas series de nudos casi idénticos, mostrando que la información estaba copiada de unos a otros de la misma manera que los monjes copistas del medievo reproducían los manuscritos a mano.
El contenido extranumérico de los quipus llamó la atención hace una década a través de la investigadora Laura Laurencich Minelli, de la Universidad de Bolonia. Esta investigadora anunció la existencia de un manuscrito titulado Historia et rudimenta linguae piruanorum, del siglo XVII, aparentemente perteneciente a los jesuitas Joan Antonio Cumis y Joan Anello Oliva, y que contiene información detallada sobre los quipus literarios. El documento incluye tres páginas de dibujos firmados por el jesuita mestizo Blas Valera, así como un sobre que contiene un fragmento de quipu.
Según el controvertido documento, algunos quipus, nombrados "reales", se diferenciaban de los que se usaban como registros por tener codificadas sílabas de algunas palabras en quechua. Sin embargo, no existen reglas bien establecidas, como en el caso de los números. De todos modos, parece que las palabras están determinadas por la combinación de la forma de los nudos, sus posiciones y colores.
Más acerca de la codificación de un lenguaje
El grado de complejidad de un lenguaje se puede relacionar con la "cantidad de cosas" que abarca un solo símbolo. Se sabe que el lenguaje es una convención entre un grupo de individuos para asignar una relación entre un símbolo y un objeto o idea. La convención del lenguaje puede entenderse como un código y, a reserva de lo que los expertos en semiótica opinen, puede relacionarse la complejidad de un lenguaje con el grado de complejidad de una comunidad, pueblo o civilización.
Se puede entonces argumentar que la escritura ideográfica es menos evolucionada, pues un solo símbolo representa varias ideas, mientras que en los idiomas occidentales cada palabra está definida de manera unívoca, salvo excepciones. Un pictograma es una imagen simple que representa una idea completa; por ejemplo, "aquí está el baño" o "no pase por aquí”. El ideograma representa una palabra, esto es, un conjunto de fonemas con un significado. Es decir, es más específico que un pictograma y, por tanto, dentro de nuestra argumentación, más complejo. Más allá de las palabras, a las letras les corresponde un sonido específico y único y se requiere un número finito de símbolos para representar una palabra. En este sentido, este tipo de lenguaje (el escrito) sería el más complejo de los tres mencionados.
En el mundo de las computadoras, una letra se representa por un conjunto de números, y más allá de posiciones numéricas, como en el código binario. Puede decirse entonces que, según la propuesta anterior, el lenguaje de las computadoras es más complejo que los idiomas occidentales, al requerir una cierta cantidad de símbolos para representar una sola letra o número. La cantidad de símbolos disponibles y las reglas de combinación entre símbolos juegan un papel importante en la complejidad de un lenguaje.

Esta idea puede servir para establecer una dirección de evolución para el lenguaje, diciendo que es más evolucionado cuanto más especializado está, en el sentido de cuántas cosas representa un carácter (el ideográfico, en que un signo representa varias palabras; binario, en que un signo representa una parte o fracción de una palabra). Cabe especular entonces acerca del grado de evolución del lenguaje escrito de los incas, puesto que se cree, como se ha mencionado antes, que el quechua era sólo el idioma hablado, mientras que el manejo abstracto de los quipus estaba confinado a unos cuantos. Los incas tenían la posibilidad de imprimir, en un simple nudo, varias dimensiones de un código, a saber: la posición, la complejidad y la dirección del nudo y el color del mismo. Así, podría pensarse que un solo nudo es un símbolo individual que abarca varios significados, pero también puede pensarse que un nudo es una manera de almacenar tres o más caracteres o posiciones de código; es decir, que un color representa una regla condicional y que diferentes colores representan números o fonemas o tal vez ideas, combinando así varias dimensiones del lenguaje escrito.
Recientemente se han dado a conocer investigaciones muy interesantes respecto a la variación cultural (Chua y colaboradores, 2005), que puede ser incluso genética, de la percepción visual. En particular, los norteamericanos de origen europeo tienden a poner más atención visual en los objetos del plano principal, mientras que los asiáticos perciben las imágenes sin eliminar por completo los objetos secundarios. Esto podría estar relacionado con la manera en la cual las civilizaciones humanas desarrollan escrituras. Tal vez los incas tenían una habilidad de percepción global de las características de los quipus que les permitía leer con bastante velocidad sus "libros".
Epílogo
Siete de los 21 quipus hallados en Puruchuco guardan una curiosa relación entre sí. La relación entre estos quipus podría representar evidencia del desplazamiento vertical de información en la estructura administrativa del imperio inca. Existen varios pares (o parejas) de quipus que poseen secuencias numéricas iguales o muy cercanamente afines. Ocasionalmente, algunos quipus completos parecen haber sido duplicados y, con mayor frecuencia, una parte de un quipu reproduce o es correlativa con un segmento dado de otro quipu. Un quipu procedente de Chachapoyas, particularmente amplio y grande, el cual se cree representa un calendario, incorpora información igualmente contenida en otros dos quipus menores procedentes de Leymebamba.
El "Proyecto de base de datos de khipu" se inició en 2002, y tiene como meta la recolección de toda la información conocida respecto a los quipus para integrarla en un sitio centralizado. Poseer los datos e información en forma digital permite a los investigadores formular preguntas acerca de los quipus que hasta ahora hubieran sido extremadamente difíciles, si no imposibles, de responder. El Proyecto de base de datos de khipu fue financiado durante el periodo 2002-2004 por la National Science Foundation estadounidense y la Universidad de Harvard, y en 2005 es financiado por la National Science Foundation, también estadounidense.
Bibliografía
Arellano, C. (1999), "Quipu y Tocapu: Sistemas de comunicación Inca", en Los incas: arte y símbolos, F. Pease y colaboradores (editores), pp. 215-262, Lima, Banco de Crédito del Perú.
Chua, H. F., J. E. Boland, y R .E. Nisbett (2005), "Cultural variation in eye movements during scene perception", Proc. Nat. Ac. Sci.102: 12629-12633.
Domenici, V. y D. Domenici (1996), "Talking knots of the inka", Archaeology 49(6): 50-56.
Fossa, L. (2005),"Los khipu: el estado de la cuestión", diario El Peruano, sección "Identidades", 7 de nov. de 2005 (para obtener el archivo en formato PDF, contactar a los auto res).
Mann, C. C. (2003),"Cracking the khipu code", Science, 300: 1650-1651.
Silverman, G. (1994), El tejido andino: un libro de sabiduría, México, Fondo de Cultura Económica.
Urton, G. (2003), Signs of the Inka Khipu: Binary Coding in the Andean Knotted-String, Austin TX, The University of Texas Press. Urton, G. y C. J. Brezine (2005), "Khipu accounting in ancient Peru", Science, 309: 1065-1067.
Urton, G. y C. J. Brezine (2003-2004),"Proyecto de base de datos de khipu", accesible en internet (http://khipuka-mayuq.fas.harvard.edu/espanol/KG_Peabody_sp.html).
Hugo Cabrera Ibarra es matemático de la Universidad Autónoma de San Luis Potosí. Obtuvo la maestría y el doctorado en ciencias con especialidad en matemáticas básicas en el Centro de Investigación en Matematicas (cimat), de Guanajuato, y se incorporó como investigador de la División de Matemáticas Aplicadas y Sistemas Computacionales del Instituto Potosino de Investigación Científica y Tecnológica (IPICyT). Sus líneas de investigación son la teoría de nudos, los modelos topológicos y las aplicaciones de la topología a la teoría de la estabilización y a la enzimología. Es miembro del Sistema Nacional de Investigadores. Esta dirección de correo electrónico está siendo protegida contra los robots de spam. Necesita tener JavaScript habilitado para poder verlo.
Haret C. Rosu Barbus es investigador del IPICyT, en la División de Materiales Avanzados para la Tecnología Moderna. Fue profesor investigador en el Instituto de Física de la Universidad de Guanajuato, y anteriormente trabajó en el Instituto de Física Atómica en Bucarest, Rumania. Es miembro del Sistema Nacional de Investigadores. Esta dirección de correo electrónico está siendo protegida contra los robots de spam. Necesita tener JavaScript habilitado para poder verlo.
Luís Adolfo Torres González nació en México D.F. Fue profesor titular de la Universidad Iberoamericana en León, Guanajuato. Actualmente es estudiante de doctorado en la División de Matemáticas Aplicadas y Sistemas Computacionales del IPICyT. Esta dirección de correo electrónico está siendo protegida contra los robots de spam. Necesita tener JavaScript habilitado para poder verlo.
Juan Pablo Treviño Gutiérrez es estudiante de maestría en la División de Matemáticas Aplicadas y Sistemas Computacionales del IPICyT. Realizó estudios de licenciatura en la Universidad de Las Américas-Puebla, con una tesis acerca de los efectos de autoimagen en fibras ópticas. Esta dirección de correo electrónico está siendo protegida contra los robots de spam. Necesita tener JavaScript habilitado para poder verlo.
Cambio de uso del suelo y degradación ambiental
Cambio de uso del suelo y degradación ambiental
Leopoldo Galicia, Arturo García Romero, Leticia Gómez-Mendoza y M. Isabel Ramírez
![]()
El control del ciclo celular en plantas
| El c o n t r o l | |||
| del ciclo celular | |||
| en plantas | |||
| Juan G. Colli-Mull, Luis Carlos Rodríguez Zapata, Enrique Castaño de la Serna |
|||
|
|
|||
|
Introducción |
|||
|
|
|||
| Figura 1. Organización estructural y propiedades de la familia de E2F en Arabidopsis. En la familia de E2F se conservan los dominios de unión al ADN, de dimerización, de caja de marcaje y el dominio de transactivación. Basado en la conservación de los diferentes dominios, las ocho proteínas de E2F de Arabidopsis son clasificadas en E2F, DP y DEL. |
|||
|
Una ruta análoga de E2F/pRb en la transición G1-S del ciclo celular, que involucra la fosforilación de pRb por los complejos CDK/ciclina y la liberación de E2F, ha sido dilucidada recientemente en células vegetales, y probablemente los mecanismos de su regulación sean los mismos que en sus contrapartes en humanos y otros eucariontes superiores (Figura 2). Aunque no se han encontrado homólogos de las ciclinas E en plantas, fundamentales en la transición G1-S en animales, las ciclinas tipo A o quizá algunas del tipo D podrían participar en la regulación de la transición G1-S y de G2-M del ciclo celular (Wen-Hui Sen, 2001). |
|||
|
Figura 2. Modelo propuesto para la regulación de la transición G1-S del ciclo celular en plantas. La expresión de las ciclinas D es estimulada por señales del medio ambiente y de crecimiento. Estas ciclinas se pueden asociar a la CDK-A. Este complejo activo ciclina D/CDK-A puede fosforilar a la Rb, la cual se encuentra formando un complejo con E2F/DP, inhibiendo la transcripción. Conforme avanza el ciclo celular, Rb es hiperfosforilada por el complejo ciclina D/CDK-A en G1 tardía, lo que ocasiona que se libere el complejo transcripcional E2F/DP, el cual es capaz de activar la transcripción de genes requeridos para la fase S del ciclo celular. |
|||
|
Genes regulados por E2f que participan en el ciclo celular |
|||
|
|
|||
|
|
|||
|
Juan Gualberto Colli-Mull es licenciado en Biología por el Instituto Tecnológico Agropecuario No. 2, y maestro en Ciencias y Biotecnología de plantas por el Centro de Investigación Científica de Yucatán (cicy). Actualmente está cursando el doctorado en Ciencias y Biotecnología de Plantas en el CICY. Su trabajo se centra en el estudio de la función de E2F en procesos de desarrollo y apoptosis en cultivos in vitro de Coffea canephora. Esta dirección de correo electrónico está siendo protegida contra los robots de spam. Necesita tener JavaScript habilitado para poder verlo. |
|||
|
Bibliografía |
|||
¿Para qué sirve la endogamia?
| ¿Para qué sirve | |
|
la endogamia?
Fidel Márquez Sánchez
|
|
|
La endogamia, que el diccionario define como el “cruzamiento entre individuos de una raza, comunidad o población aislada genéticamente”, se caracteriza técnicamente como la condición homocigótica de genes en un determinado sitio (locus) cromosómico. |
|
|
|
Lo malo de la endogamia El efecto perjudicial de la endogamia, también llamado “depresión endogámica”, necesariamente tuvo que ser observado por el ser humano, probablemente dentro del mismo grupo al que pertenecía, al descubrir que los hijos (progenie) de parejas emparentadas mostraban anomalías como enanismo, albinismo, hemofilia, etcétera, que se acentuaban a lo largo de las generaciones. Para evitarla debió comenzar a hacer precisamente lo contrario del apareamiento endogámico, es decir, procurar que los cruzamientos se hicieran entre individuos no emparentados. |
|
Al reconocer el efecto de la endogamia en las poblaciones de animales o plantas que explotaba, el ser humano comenzó a “refrescar la sangre” mediante apareamientos con miembros de otras poblaciones no emparentadas y diferentes a las suyas. En las ganaderías empresariales se procura conocer el pedigrí de los pies de cría; es decir, se hace una selección de los progenitores. De hecho, podemos decir que las formas para evitar la endogamia (o “consanguinidad”, como prefieren llamarla los zootecnistas y ganaderos) tuvieron lugar primero en la cría y explotación del ganado, ya que en los animales sus efectos son más evidentes que en los cultivos agrícolas. |
|
|
|
|
|
De que los genes en un locus de un individuo sean idénticos a los genes de un locus de otro individuo. Por lo tanto, la coancestría entre dos progenitores es igual a la endogamia de su progenie. De hecho, en la práctica, la endogamia de una progenie es igual a la coancestría de sus progenitores. Por ejemplo, si X y Y son los progenitores de Z, entonces rXY = FZ |
|
|
|
|
|
Los resultados de un estudio de Márquez (1992) sobre la endogamia en los sintéticos mostraron que mientras mayor era el número de líneas (de 2 a 1) la reducción de la endogamia era de casi 0 a 80 por ciento para cualquier grado de endogamia de las líneas, mientras que si se aumentaba el número de plantas por línea (de 1 a 10), las reducciones eran de 90 por ciento para plantas no endogámicas, 45 por ciento para líneas fraternales, 50 por ciento para líneas S1 y 0 por ciento para líneas homocigóticas. |
|
|
|
|
|
Incremento del germoplasma de maíz |
|
 |
|
|
Entonces, ¿para qué sirve la endogamia? |
|
| Bibliografía Busbice, T. H. (1969), "Inbreeding in synthetic varieties", Crop Sci. 9:601-604. Busbice, T. H. (1970), "Predicting yield of synthetic varieties", Crop Sci. 10:260-269. Falconer, D. S. (1967), Introduction to quantitative genetics, Oliver and Boyd, Londres, pp.85-93. Márquez Sánchez, F. (1988), Genotecnia vegetal II, AGT Editor, México, 665 p. Márquez-Sánchez, F. (1992), "Inbreeding and yield prediction in synthetic varieties of maize cultivars made with parental lines: I. Basic methods", Crop Sci. 32:345-349. Márquez-Sánchez, F. (1998), "Expected inbreeding with recurrent selection in maize: I. Mass selection and modified ear-to-row selection", Crop Sci. 38:1432-1436. Márquez-Sánchez, F. (1999), "Accumulated inbreeding in maize germplasm reproduction", Maydica 44:225-229. Márquez-Sánchez, F. (2005), "Derivation of open-pollinated inbred lines, and their relation to Z lines for cyclic hybridización", Arnel R. Hallauer international symposium in plant breeding, CIMMYT, agosto17-22 (acepta-do para publicación). Wright, S. (1921), "Systems of mating II. The effects of inbreeding on a genetic composition of a population", Genetics 6:124-143. |
|
| Fidel Márquez Sánchez es ingeniero agrónomo egresado de la Escuela Nacional de Agricultura en 1958. Obtuvo la maestría y el doctorado en la Iowa State University. Es doctorado honoris causa y agrónomo ilustre de la Universidad Autónoma de Chapingo, y fellow de la American Society of Agronomy. Pertenece a la Academia Mexicana de Ciencias y al Sistema Nacional de Investigadores. Desde hace 14 años trabaja en el Centro Regional Universitario de Occidente de la Universidad Autónoma de Chapingo, en Guadalajara, Jalisco, en el campo de mejoramiento genético de maíces criollos e hibridación. Esta dirección de correo electrónico está siendo protegida contra los robots de spam. Necesita tener JavaScript habilitado para poder verlo. | |
Noticias de la Academia
|
Noticias de la |
|||
| Academia | |||
| Olimpiadas de la Ciencia | |||
| Triunfa México en competencias internacionales de ciencias | |||
|
Este año la Academia Mexicana de Ciencias obtuvo varias medallas en competencias internacionales, entre ellas la medalla de oro en el Octavo Campeonato Mundial de National Geographic, cuya final se celebró el pasado 9 de agosto, en el SeaWorld de San Diego, California, dejando al equipo de Estados Unidos -el anterior campeón- en el segundo sitio y a Canadá en tercero. |
|||
|
Carlos Bosch Giral, coordinador de la Competencia Cotorra y del Concurso de Primavera de Matemáticas, mencionó que estos resultados son sólo la punta del iceberg del esfuerzo conjunto y del trabajo en equipo que involucra a la AMC, a profesores y a familiares, y que ahora rinde sus frutos con medallas internacionales. |
 |
||
| Los adolescentes y jóvenes triunfadores, junto al Dr. Juan Pedro Laclette, de visita en las instalaciones de la AMC. | |||
|
Consejo directivo |
|||
| Crean fondo para apoyar a jóvenes con talento científico | |||
|
El presidente de México, Felipe Calderón, anunció la creación de un fondo de becas para apoyar a los ganadores de las olimpiadas científicas con el objetivo de impulsar su talento, que será coordinado por la Academia Mexicana de Ciencias (AMC) y la Secretaría de Educación Pública (SEP). Al respecto, Juan Pedro Laclette, presidente de la AMC, subrayó que la organización de las olimpiadas, junto con la detección de jóvenes |
|||
|
|
Felipe Calderón anunció la creación del fondo, durante la visita de los ganadores del Octavo Campeonato de National Geographic a Los Pinos. |
||
|
Novedad editorial |
|||
| Rinden homenaje a pioneras de la ciencia en México | |||
| La Academia Mexicana de Ciencias (AMC), el Consejo Consultivo de Ciencias de la Presidencia de la República y el Consejo Nacional de Ciencia y Tecnología rinden homenaje a mujeres científicas con el quinto volumen de la serie Ciencia y tecnología en México en el siglo XX. Presentado en junio pasado, el libro Biografías de personajes ilustres, dedicado a mujeres forjadoras de la ciencia y la tecnología mexicanas, describe las carreras de 14 investigadoras mexicanas, cinco de ellas dedicadas a las ciencias naturales y exactas y otras nueve enfocadas al ámbito de las ciencias sociales y humanidades. Juan Pedro Laclette, presidente de la AMC, mencionó que, si bien a mediados del siglo pasado la mujer se integró al campo laboral y se han reducido las diferencias entre ambos sexos, aún hay mucho que hacer. Por ello, la Academia mantiene un enfoque de género en todo momento. "La AMC cuenta entre sus integrantes con un mayor porcentaje de mujeres que otras academias del primer mundo, con un 21 por ciento", afirmó Laclette. "En academias de ciencias europeas como las de Francia, Alemania y Dinamarca, entre otras, el porcentaje de mujeres es mucho más bajo". |
|||
|
|
|||
|
El quinto volumen de la serie Ciencia y Tecnología |
|||